Доброго времени суток!
Вы ищете условие, при котором для заданной матрицы

(размером K x N, состоящей из N столбцов-векторов в

) существует такой вектор весов

в

, что результирующий вектор

удовлетворяет двум условиям:
1. Все его компоненты неотрицательны:

(то есть

для всех

).
2. Сам вектор

не является нулевым:

(то есть хотя бы одна компонента

строго положительна).
Задача действительно имеет общие черты с задачами линейного программирования (линейные операции, линейные ограничения в виде неравенств), но, как Вы верно заметили, здесь отсутствует целевая функция для оптимизации. Мы имеем дело с задачей о разрешимости определённой системы линейных соотношений. Множество всех возможных линейных комбинаций

образует образ (или пространство столбцов) матрицы

, являющийся линейным подпространством

. Вопрос заключается в том, содержит ли это подпространство ненулевые векторы, принадлежащие неотрицательному ортанту

.
Для анализа таких систем существуют мощные инструменты, известные как
теоремы об альтернативе. Наиболее известной из них является лемма Фаркаша, но для Вашей задачи более точно подходит следующая формулировка (иногда связываемая с теоремой Гордана или другими теоремами об альтернативе):
Теорема. Для любой матрицы

(размером K x N) ровно одна из следующих двух систем имеет решение:
1.
(Исходная задача) Существует

в

такой, что

и

.
2. Существует

в

такой, что

и

(то есть

для всех

).
(Здесь

обозначает транспонированную матрицу

).
Таким образом, Ваша исходная задача (система 1) имеет решение тогда и только тогда, когда система 2
не имеет решения. Иными словами, критерий разрешимости Вашей задачи таков:
Не должно существовать вектора  со всеми строго положительными компонентами, который был бы ортогонален всем строкам матрицы
со всеми строго положительными компонентами, который был бы ортогонален всем строкам матрицы  (или, что эквивалентно, принадлежал бы левому ядру матрицы
(или, что эквивалентно, принадлежал бы левому ядру матрицы  , т.е.
, т.е.  , или ядру
, или ядру  , т.е.
, т.е.  )
).
Давайте проверим Ваши примеры с помощью этой теоремы.
Пример  .
.Матрица

. Ищем

с

такой, что

.
Уравнение:

.
Такой вектор существует, например,

(здесь

).
Следовательно, система 2 имеет решение, а значит, система 1 (Ваша задача) решения
не имеет. Это совпадает с Вашей классификацией "нерешаемая".
Пример  .
.Матрица

. Ищем

с

такой, что

.
Система уравнений:


Из второго уравнения

. Поскольку мы требуем

, то

должен быть отрицательным (

). Это противоречит требованию

.
Следовательно, система 2
не имеет решения (невозможно удовлетворить всем условиям одновременно).
Согласно теореме, система 1 (Ваша задача)
должна иметь решение. Вы классифицировали эту матрицу как "нерешаемую", что, возможно, является результатом того, что найти подходящий вектор

не всегда очевидно. Однако решение существует. Например, если взять

, то

. Этот вектор

удовлетворяет условиям

и

.
Пример  (предполагая опечатку в вашем изображении, где
(предполагая опечатку в вашем изображении, где  ).
).Матрица

. Ищем

с

такой, что

.
Уравнение:

. Это уравнение не имеет решений при

.
Значит, система 2 не имеет решения, а система 1
имеет решение. Например,

, что дает

, удовлетворяющий условиям

и

. Это совпадает с Вашей классификацией "решаемая".
Пример  .
.Матрица
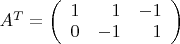
. Ищем

с

такой, что

.
Система уравнений:


Подставляя второе уравнение в первое:

. Это противоречит требованию

.
Значит, система 2
не имеет решения. Следовательно, система 1 (Ваша задача)
имеет решение. Ваше наблюдение, что сумма столбцов (

) дает

, подтверждает это (

и

).
Относительно Вашего наблюдения.Ваше наблюдение о том, что матрица "решаема", если у нее есть столбец, все элементы которого одного знака (и не все нули), совершенно верно и является
достаточным условием.
* Если есть столбец

(j-й столбец матрицы

) такой, что

для всех

и

, то можно взять

(j-й вектор стандартного базиса). Тогда

. Очевидно,

и

.
* Если есть столбец

такой, что

для всех

и

, то можно взять

. Тогда

. Очевидно,

и

.
Однако, как показывают примеры

(который оказался решаемым) и

, это условие не является
необходимым. В этих матрицах нет столбцов, удовлетворяющих данному свойству, но задача тем не менее имеет решение.
Общий и точный критерий разрешимости Вашей задачи сводится к проверке несуществования строго положительного вектора

в (левом) ядре матрицы

(или, эквивалентно, в ядре

). Проверка этого условия может быть выполнена, например, с помощью методов линейного программирования (попытаться найти такой

, минимизируя, скажем,

при условиях

,

для некоторого малого

).