Устойчивость движения

[drzewo]

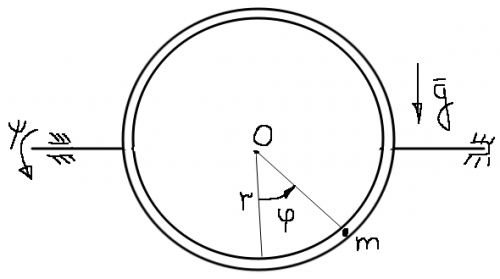
Тонкая однородная трубка массы $M$ в форме кольца радиуса $r$ может свободно вращаться вокруг своего горизонтального диаметра. В трубке находится дробина массы $m$, которая может свободно кататься по внутренности трубки.
Очевидно, в системе имеются решения при которых $ \varphi(t)\equiv 0$, а $\psi(t)$ -- монотонно возрастает.
Верно ли, что при достаточно больших $\dot\psi(0)$ эти решения устойчивы по Ляпунову? Насколько большим надо брать $\dot\psi(0)$?

К ответу на этот вопрос можно подходить разными способами, но думаю, что точных оценок не будет:)

[Padawan]

drzewo в сообщении #1675591 писал(а):

Верно ли, что при достаточно больших $\dot\psi(0)$ эти решения устойчивы по Ляпунову? Насколько большим надо брать $\dot\psi(0)$?

Вроде бы очевидно, что не будет устойчиво по Ляпунову, потому что небольшая разница в начальной угловой скорости кольца приведет со временем к большой разнице самого угла $\psi(t)$, так как периоды обращения будут различны. Тут, видимо, какое-то другое понятие устойчивости подойдет (орбитальная устойчивость?)

[drzewo]

Понизим порядок гамильтоновой системы с помощью интеграла энергии

$$H=\frac{p_\psi^2}{2(J+mr^2\cos^2\varphi)}+\frac{p_\varphi^2}{2mr^2}-mgr\cos\varphi\cos\psi=h;\quad J=mr^2/2$$

получим систему с гамильтонианом $\mathscr H$ в новом времени $\tau=-\psi$

$$ \mathscr H=\sqrt{2(J+mr^2\cos^2\varphi)\Big(h-\frac{p_\varphi^2}{2mr^2}+mgr\cos\varphi\cos\tau\Big)} $$

Разумно ставить вопрос об устойчивости по Ляпунову решения $p_\varphi(\tau)= 0,\quad \varphi(\tau)= 0$ при достаточно большом $h$

-- 20.02.2025, 16:23 --

Грубая, неформальная прикидка состояла бы в том что бы посмотреть насколько большим должно быть $h$ чтобы мультипликаторы лежали на единичной окружности.

[drzewo]

дальше КАМ:)

[Padawan]

drzewo в сообщении #1675667 писал(а):

получим систему с гамильтонианом $\mathscr H$ в новом времени $\tau=-\psi$

drzewo
Подождите, я мало что понял, из того, что Вы написали. Но прав ли я, что устойчивости по Ляпунову не будет, но имеет смысл исследовать устойчивость в следующем смысле:

$$ \forall\varepsilon>0\,\exists\delta>0:\forall x, |x-x_0|<\delta\,\forall t>0\,\exists\tau>0: |g^t(x_0) -g^\tau(x) |<\varepsilon, $$

где $g^t(x)$ -- оператор сдвига по траекториям за время $t$?

[drzewo]

Padawan в сообщении #1675706 писал(а):

Но прав ли я, что устойчивости по Ляпунову не будет,

думаю, да, правы.

Padawan в сообщении #1675706 писал(а):

но имеет смысл исследовать устойчивость в следующем смысле:

$$ \forall\varepsilon>0\,\exists\delta>0:\forall x, |x-x_0|<\delta\,\forall t>0\,\exists\tau>0: |g^t(x_0) -g^\tau(x) |<\varepsilon, $$

не знаю, мне не очевидно, что такая устойчивость должна быть

[Theoristos]

А если перейти в с.к. связанную с кольцом?

[drzewo]

Padawan в сообщении #1675706 писал(а):

Подождите, я мало что понял, из того, что Вы написали

Я написал, как изучать орбитальную устойчивость решения относительно возмущений начальных данных , лежащих на том же уровне энергии , что и само решение.

-- 23.02.2025, 20:54 --

Про понижение порядка гамильтоновой системы с помощью интеграла энергии см. Арнольд Мат методы класс. мех.