Что такое многоугольник в формуле Кристоффеля-Шварца

[Red_Herring]

Отобразить конформно $\mathbb{C}_+:= \{z\colon \operatorname{Im} (z)>0\}$ на многоугольник. Формула К-Ш

$$F'(z)=\prod _{j=1}^n (z- x_j)^{-1+\alpha_j/\pi} $$

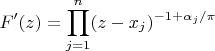
где $\alpha_j$ внутренние углы.

Но что такое многоугольник? Прежде всего предположим что МУ д.б. односвязным. Если МУ связен и ограничен (разрезы допустимы) К-Ш применима. Иногда она применима и для неограниченных МУ.

Например, для $1$-гольниов $\mathbb{C}\setminus [0,\infty)$, для $2$-угольников $P= \{z\colon -1<\operatorname{Re} (z)< 1,\ \operatorname{Im} (z)>0\}$ и $\mathbb{C}\setminus P$, для $3$-угольника $\mathbb{C}_+ \setminus [0,ai], \ a>0$ и подобных, где углы только конечные.

Но для $2$-угольников $\mathbb{C}\setminus [-1,1]$ и $\mathbb{C} \setminus ((-\infty, -1]\cup [1,\infty))$ К-Ш не работает. Разумеется, я знаю соответствующие комформные отображения, но они не К-Ш.

МУ д.б. односвязным как подмножество комплексной плоскости $\mathbb{C}$, а не расширенной комплексной плоскости $\mathbb{C}\cup\{\infty\}$. Но $\mathbb{C} \setminus ((-\infty, -1]\cup [1,\infty))$ односвязен. Да

$$F'(z)= (z-1)(z+1)/z^2$$

работает. Значит ли это что мы можем взять

$$F'(z)=\prod _{j=1}^n (z- x_j)^{-1+\alpha_j/\pi} z^{-s}?$$

Например для $\mathbb{C}\setminus ((-\infty,-1] \cup [1,\infty) \cup (-\infty i,-i] \cup [i,\infty i))$?

[Утундрий]

Red_Herring в сообщении #1668533 писал(а):

что такое многоугольник?

Имхо, в данных циркумстанциях, нечёткое понятие "много" разумно начинать с трёх.

[makxsiq]

(Оффтоп)

Некоторые с нуля начинают. Вот например $V(0)=1$.