Магнетон Бора

[tsapel]

Магнетон Бора определяется в модели атома Бора как орбитальный магнитный момент электрона в основном состоянии атома водорода.
Основное состояние атома водорода в квантовой физике соответствует квантовым числам n=1, l=0, m=0. В этом состоянии орбитальный квантовый момент импульса и орбитальный магнитный момент электрона равны 0.
Помогите разобраться какому магнитному моменту в квантовой физике соответствует магнетон Бора?

[DimaM]

В модели Бора у электрона в основном состоянии момент импульса $L=\hbar$. Отсюда по известной формуле $m=eL/(2m_ec)$ получается соответствующий магнитный момент.
К основному состоянию настоящего атома водорода отношение имеет сугубо историческое.

[tsapel]

DimaM в сообщении #1663727 писал(а):

К основному состоянию настоящего атома водорода отношение имеет сугубо историческое

- это об основном состоянии атома водорода в квантовой физике?
Я предполагал, что одни и те же объекты (атом водорода, ядро, электрон) в разных моделях (планетарная Резерфорда, квазиклассическая Бора, квантовая) имеют соответствующие характеристики. И в квантовой физике и в модели Бора предполагается квантование магнитного момента электрона (дискретные значения).
В модели Бора дискреты кратны магнетону Бора и в основном состоянии (на орбите, наиболее близкой к ядру) магнитный момент электрона равен одному магнетону. В квантовой физике основное состояние характеризуется квантовыми числами n=1, l=0, m=0, при которых максимальная плотность вероятности электрона достигается на расстоянии от ядра, соответствующем орбите магнетона Бора (подуровень 1s). Но на этом уровне орбитальный магнитный момент равен 0.
Вот у меня и возник вопрос. Основные состояния в моделях квантовой и Бора вроде соответствуют друг другу. А вот значения в основном состоянии орбитального магнитного момента и магнетона Бора кардинально различаются. И первый орбитальный магнитный момент, отличный от 0, возникает при n=2 (возбужденное состояние). Это действительно так или я допускаю ошибку в рассуждениях.

[DimaM]

tsapel
Я не совсем понимаю, чего вы хотите.
Модель Бора дает правильные энергии и неправильные моменты импульса. Нынче имеет в основном историческую ценность.
Термин магнетон Бора появился примерно в то же время, имеет совершенно ясный физический смысл.
Магнетон Бора - это просто величина, в настоящая время она не связана с каким-то конкретным состоянием какого-то конкретного атома.

[Cos(x-pi/2)]

tsapel

"Планетарная модель Резерфорда" и "модель атома Бора" - это исторические вехи, важные постольку, поскольку они в то давнее время подтолкнули учёных к зарождению квантовой физики. Но на роль согласующихся с опытом моделей в современной физике они не годятся.

Модель атома Бора, как выяснилось в ходе создания последовательной квантовой теории, даёт в целом неправильную картину. Она не соответствует современной квантовой механике, созданной после введения Шрёдингером понятия "волновая функция" и "уравнения Шрёдингера". Затем в поисках релятивистского обобщения было открыто уравнение Дирака, и стала развиваться квантовая электродинамика. Так что, теперь в физических (а не исторических) формулировках не следует опираться на модель атома Бора. Да, Бор ввёл в дело важные комбинации мировых констант, и за ними закрепилось его имя, - "радиус Бора", "магнетон Бора", - но теперь они определяются уже из других соображений.

Если у Вас нет под рукой подходящих учебников, то попробуйте посмотреть, например, "Краткий курс теорфизики" Ландау и Лифшица (сканы в формате djvu доступны на этой странице библиотеки eqworld):

Ландау Л.Д., Лифшиц Е.М. Краткий курс теоретической физики, том 1: Механика. Электродинамика.

Ландау Л.Д., Лифшиц Е.М. Краткий курс теоретической физики, том 2: Квантовая механика.

В томе 1, § 66 "Магнитный момент", формула (66,5), речь идёт о классической (т.е. не квантовой) системе точечных зарядов с нерелятивистскими скоростями $v\ll c.$ Если у всех зарядов системы отношение заряда к массе ($e/m)$ одинаково, то магнитный момент системы $\mathbf{m}$ связан с её механическим моментом $\mathbf{M}$ равенством

$$\mathbf{m}=\frac{e}{2mc}\,\mathbf{M}\,,$$

т.е. отношение магнитного момента к механическому постоянно и равно $e/(2mc).$

В томе 2, § 43 "Частица в магнитном поле" говорится, что частица со спином $s$ ($s$ это безразмерное число, у квантовых частиц разного сорта спин равен $0,\,1/2,\, 1,\, ...)$ обладает "собственным" (т.е. не связанным с орбитальным состоянием частицы) моментом импульса величиной $M=\hbar s$ и "собственным" же магнитным моментом, величина $\mu$ которого пропорциональна $M.$

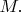
Эксперименты показывают, что отношение собственного магнитного момента $\mu$ к собственному механическому моменту $\hbar s$ у квантовых частиц не совпадает с классическим $e/(2mc).$

У электрона это отношение оказалось почти равным (с точностью порядка $0.001)$ вдвое большей величине, т.е. $|e|/(mc).$ Здесь $m$ - масса электрона, $e$ - заряд электрона. Спин электрона равен $1/2,$ так что его собственный момент импульса равен $\hbar /2,$ и, значит, абсолютная величина собственного магнитного момента $\mu$ электрона с точностью порядка десятой доли процента даётся формулой

$$\mu \approx \frac{|e|}{mc}\,\frac{\hbar}{2}\,=\,\frac{|e|\hbar}{2mc}$$

Величину $\mu_B=|e|\hbar /(2mc)$ называют магнетоном Бора.

Точное равенство $\mu=\mu_B$ получается теоретическим путём из уравнения Дирака для электрона; см. том 2, § 93 "Магнитный момент электрона".

(Речь у нас идёт об абсолютной величине $\mu$ магнитного момента; пишем $|e|$, так как заряд электрона отрицательный: $e<0.)$

Уравнение Дирака даёт для $\mu$ значение $\mu=\mu_B,$ лишь приближённо соответствующее эксперименту, потому что это уравнение не учитывает полностью эффекты квантовой электродинамики. Если же их учесть, то в первом порядке малости по $\alpha$ (это постоянная тонкой структуры) получается формула Швингера, см. том 2, § 105 "Радиационные поправки":

$$\mu=\frac{|e|\hbar}{2mc}\left( 1+\frac{\alpha}{2\pi}\right)$$

Здесь величина в скобках приблизительно равна $1.00116$ в хорошем согласии с опытом. (При учёте поправок более высокого порядка по $\alpha$ соответствие квантовой электродинамики с опытом ещё улучшается.)

[tsapel]

Ну просто забавно получается.
Магнетон Бора естественно определяется из модели Бора, соответствует орбитальному магнитному моменту атома водорода в основном состоянии и имеет вполне определённую характеристику длинны (радиус орбиты).
В квантовой физике основному состоянию атома водорода уже соответствует только радиус орбиты магнетона Бора. Соответствие магнетона Бора собственному магнитному моменту электрона устанавливается уравнением Дирака и используется только его модуль. А собственно (не собственный) орбитальный момент электрона в основном состоянии оказывается равным 0.
Я не ошибаюсь?