Ostensibly, the seriousness of this question is not yet realized.
The issue is that if we let the solution to be of the form
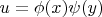
, then we get
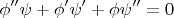
which doesn't seem to separate out. However, if we let the solution to be of the form
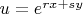
, then substitution yields
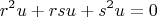
Which solves out to give the following two families of the solutions:

That is, the solution is of the form
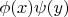
.
Again, if we let the solution to be of form
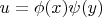
and assume

to be linear that is its second derivative vanishes, then indeed the equation will be separable.
Therefore, it seems as if the property of separability is not inherent in the equation itself rather it is about what form we choose for our sample solution, unlike the case of matrices. A matrix is invertible (or not invertible) irrespective of what determinant function we define, the invertibility is inherent in the matrix itself.
-- 21.09.2024, 19:37 --daise equation
А что это значит?
At other places we simply call it typo.