Т.е. нам нужна функция

, и значения которой на данном наборе из

аргументов все разные?
Да.
А зачем тогда все рассказы про 3 одинаковых бита?
Просто человек мыслит битами и байтами (как и я), а не математическими абстракциями. И числа кодирует двумя байтами, т.е. реально ему надо

. Но он точно знает что какие-то 6 битов из 16 в каждом числе фиксированы и всегда одинаковы для интересующего его набора чисел, потому 16 можно уменьшить до 10.
Соответственно попытка сделать хеш-функцию параметризованную меньше чем 129 битами обречена на провал.
Это если её вычислять по заданному набору чисел. Но всегда есть надежда наткнуться на подходящую функцию случайно (взяв например младшие нечётные биты из MD5 от входного числа). Или можно подобрать (тоже почти случайно) пару-тройку таких функций, коллизии которых компенсируют друг друга. В конце концов даже если одна функция обрабатывает всего 70% входных чисел (как в общем у меня получалось), т.е. оставляет треть (

) не обработанными, то составив 5 разных функций подряд снизим вероятность коллизии до

, т.е. коллизии могут быть, но их вероятность невелика. Но функции нужны (линейно) независимые. Я не вполне уверен что остаток от деления на взаимно простые числа подходит и уж тем более что уложится суммарно в 7 бит.
Мне потому и кажется что тут больше вопрос кодирования чем математических функций, что можно поискать как поэффективнее кодировать числа, может они как-то похожи друг на друга (вдруг они все кратны 5 или 13, или для этого надо битовую запись перевернуть) (или например можно несложным преобразованием их к такому виду привести, скажем переходя к разностям или xor или реверсом битов или разделением на чётные и нечётные биты или более сложной функции) и тогда можно придумать более эффективный алгоритм преобразования, не перебирая все эти

вариантов. Но надо знать сами числа и искать чем они похожи.
было предложено использовать хеш-функции, но как выяснилось, здесь это не работает.
Работает, только найти подходящую хэш-функцию весьма и весьма сложно. Но разбив её на две-три - найти уже легче. Хотя я всё равно сомневаюсь в успехе.
Можно искать бинарным поиском, но вероятности получаемых символов сильно отличаются, и не соответствуют порядку сортировки. Почти всегда потребуется 7 обращений к массиву.
Можно в массиве хранить лишь младшие биты входных чисел, а выделять нужный кусок в основном массиве по второму массиву, индексом в котором будут оставшиеся старшие биты. Тогда 4 старших бита (табличка из 16 байтов) дают один из 16 кусков внутри основной 120 байтовой таблички в среднем длиной в 15 элементов или 3-5 обращения (5 максимум, почти в половине случаев хватит 3 или 4), всего 4-5 обращений к двум массивам. Если куски получаются сильно разного размера, то предварительно перемешать входные числа простой хэш-функцией (типа
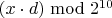
).