Я думаю, для простоты можно отвлечься от качающегося маятника и считать, что груз маятника движется поступательно, а прочие детали механизма невесомы. Метрономы можно описать каким-нибудь автоколебательным уравнением относительно

, хоть тем же ван-дер-полем, только, конечно, без вынуждающей силы. Зато благодаря установке на общую движущуюся доску в нем будет дополнительная сила инерции

. А уравнение движения самой доски записать в форме теоремы о движении центра масс (вроде бы доска катается на пивных банках свободно). Тогда


где

--- полная масса системы. Очевидно, координату доски

можно исключить, тогда в пределе
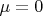
получаем линейную колебательную систему с

единичными собственными частотами и одной частотой

, причем последняя как раз соответствует синхронизованным колебаниям.
Дальше можно попробовать приближенно решать эту систему методом Уизема, как это обычно делают, но там начинается уже малоприятная бухгалтерия...