Максимум множества - это его наибольший элемент, то есть такой, который больше или равен всех остальных. Максимальный - это такой, юольше которого нет. Например, в множестве

с
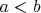
и

оба элемента

и

будут максимальными, а наибольших нет. Супремума у этого множества нет, но если добавить

такой, что

, то

будет супремумом

. Но не его максимальным элементом!