Нормальность распределений. И равенство их дисперсий 1.
1. Пусть

Тогда

имеет распределение хи-квадрат.
Никакого равенства дисперсий единице не требуется.
2. Нормальность распределений обеспечивается теоремой Пирсона, которая в свою очередь обеспечивается ЦПТ.
Как описано, например,
тутТаким образом, условия применимости критерия хи-квадрат описываются требованиями:
а) на минимальное количество элементов в выборке
б) на минимальное количество элементов "в кучке", на которые разбиваем носитель.
Никаких дополнительных требований и предположений
не требуется.
-- 04.07.2024, 19:54 --Определение этих требований - вопрос, конечно, непростой и тонкий. Но чтобы не уходить в дебри, обратимся к рекомендациям
лучших собаководов специалистов.
По приведенной выше ссылке приведена и обосновывается рекомендация, чтобы ожидаемые частоты в каждой кучке были не менее "5-6".
Для данного

и для ожидаемого распределения этого можно достичь разбиением на 6 кучек.
Таким образом, условия применимости выполняются.
-- 04.07.2024, 19:57 --Проверьте свой "метод" на "истинно-биномальных" сериях....
Давно проверил. Прекрасно работает. Можете попробовать самостоятельно.
UPD. Метод не мой, а Пирсона.
(Оффтоп)
А если Вы сделаете 100500 серий и получите 3.5
анонимуса серии, где p-value окажется меньше
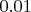
, то я Вам скажу, что у Вас множественные сравнения, на которые нужно делать поправку
