Наивные вопросы по математической статистике

[Anton_Peplov]

Здесь я буду задавать наивные вопросы по математической статистике. Вопросы задаются по одному, следующий после закрытия предыдущего.

Вопрос № 1. Сходимость по распределению и состоятельность медианы.

Читаю Лагутин М. Б. Наглядная математическая статистика. М.: Бином, 2009.. Принятые обозначения:
$\xi \sim f$ - случайная величина $\xi$ распределена по закону $f$
$\mathcal{N} (m, \sigma)$ - нормальный закон с матожиданием $m$ и СКО $\sigma$
$\overset{d}{\to}$ - сходимость по распределению.
$\operatorname{MED}$ - выборочная медиана
$x_{1/2}$ - теоретическая медиана, т.е. корень уравнения $F(x) = 1/2$.

Лагутин на с. 86-87 писал(а):

Теорема 1. Пусть элементы выборки имеют плотность $p(x)$, причем $p(x_{1/2})>0$. Тогда при $n \to \infty$

$$ \sqrt n (\operatorname{MED} - x_{1/2}) \overset{d}{\to} \xi \sim \mathcal{N} \left (0, \dfrac{1}{4p^2(x_{1/2})} \right ) $$

<...>
При выполнении условий теоремы 1 выборочная медиана будет состоятельной оценкой для $x_{1/2}$.

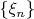
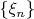
Напомню, что такое сходимость по распределению. Последовательность случайных величин $\{\xi_n\}$ порождает последовательность интегральных функций распределения $\{F_n\}$. Последовательность $\{\xi_n\}$ называется сходящейся по распределению к случайной величине $\xi$ с интегральной функцией распределения $F$, если последовательность $\{F_n\}$ сходится к $F$ во всех точках непрерывности последней.

Как я неформально понимаю эту теорему: при увеличении числа опытов закон распределения разности между выборочной и теоретической медианой будет все более похож на нормальный с матожиданием 0. Это ок. Но действительно ли отсюда следует состоятельность \operatorname{MED}$ как оценки для $x_{1/2}$? Состоятельность означает, что при увеличении числа опытов последовательность выборочных медиан сходится к $x_{1/2}$ по вероятности. В то время как в теореме речь только о сходимости по распределению. Из сходимости последовательности по распределению, вообще говоря, не следует ее сходимость по вероятности.

[Alex Krylov]

https://en.wikipedia.org/wiki/Proofs_of_convergence_of_random_variables#propB1
Сходимость последовательности случайных величин к константе по распределению влечет за собой сходимость по вероятности.