Так уж вы определитесь по конкретнее с функцией
Первый абзац (в последнем док-ве):
(a) функцию
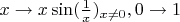
можно обозначить как

Тогда

действительно две разные функций,
или
(b)

можно спрятать и использовать по умолчанию как те же

выше.
Второй абзац (в последнем док-ве):
Все упоминания

поменять на

при условий что функцию
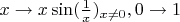
назвали

.
Будет ли точка

предельной?
Допустим

- предельная точка. Пусть

- окрестность нуля. Мы должны найти

для которой

попадает в

. Но для любой

, имеется тот факт,что

принимает значения между

и

. Тогда только

может попасть в

. В таком случае

, хотя в определений функций имеем

Поэтому мы нашли окрестность

которая не имеет

что означает

не предельна.
Неплохо бы основать, что других точек, которые надо добавить к замыканию, нет.
Чтоб доказать что больше предельных точек нет, берем какую-нибудь точку

за пределами графика и находим ей окрестность куда не попадает ни однa точка на графике. Пускай

дистанция от ближайшей точки на графике до

. Тогда

.

не на графике, но все же является предельной. Придется наити новое док-во того, что больше предельных точек нет.