Доказать утверждение, похожее на закон больших чисел

[artempalkin]

Это задача 4.11 из Севастьянова (пункт б)
Пусть функция $f(x),\ 0\leqslant x \leqslant 1$, ограничена и интегрируема, а $\xi_1,\xi_2, \cdots$ - независимые СВ, равномерно распределенные на отрезке $[0,1]$. Найти:

$\lim\limits_{n\to\infty}P\left\{\left|\frac{f(\xi_1)+\cdots+f(\xi_n)}n-\int\limits_0^1f(x)dx\right|>\frac{\varepsilon}{\sqrt n}\right\}$, $\varepsilon>0$

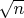
Во-первых, ясно (путем несложных вычислений), что $\int\limits_0^1f(x)dx$ - это матожидание $\frac{f(\xi_1)+\cdots+f(\xi_n)}n$. Далее тоже несложно показать, что $Df(\xi_1)$ будет конечна. Хочется тогда использовать неравенство Чебышёва, но оно принципиально не работает (как раз из-за этого $\sqrt n$)... в таком случае может возникнуть мысль явно разобрать распределение $\frac{f(\xi_1)+\cdots+f(\xi_n)}n$, но, кажется, мы маловато знаем про $f(x)$, чтобы обозримо здесь что-то сделать...

Подскажите, что можно сделать?

[Sdy]

artempalkin,
1. Если $\xi_1,\ldots, \xi_n$ -- независимые одинаково распределённые случайные величины, то что можно сказать о случайных величинах $f(\xi_1),\ldots, f(\xi_n),$ в случае "хорошей" $f$?
2. Когда Вы видите вероятность вида $\mathbb{P}(\sqrt{n}(\overline{X}_n-\mathbb{E}X_1) \leq a)$ при $a \in \mathbb{R}$, чем и при каких ограничениях Вы хотите воспользоваться для того чтобы найти эту вероятность при $n \to +\infty$?

Я здесь использую следующее обозначение : если $X_1,\ldots, X_n$ это случайные величины, то выражение $\frac{X_1+\ldots+X_n}{n}$ называют выборочным средним и обозначают как $\overline{X}_n.$

[adfg]

центральная предельная теорема