Полное решение задачи о математическом маятнике.

[Enceladoglu]

Для математического маятника закон сохранения энергии
$\frac{m\dot{\varphi}^2 l^2}{2} + mgl(1-cos \varphi) = E$
Отсюда

$$\int\limits_{ \varphi}^{ \varphi_0} \frac{dx}{\sqrt{E - mgl(1-cos \varphi) } } = \frac{2}{m} (t - t_0)$$

Обозначив $\frac{E}{2mgl} = k $ Придем вот к такому выражению:

$$\int\limits_{ \varphi}^{ \varphi_0} \frac{d\varphi/2}{\sqrt{k^2 - sin^2(\varphi/2) } } = \sqrt{\frac{g}{l}}(t - t_0)$$

Далее делается замена $ k sin \theta = sin (\varphi/2)$ и мы приходим к такому

$$\int\limits_{ \theta}^{ \theta_0} \frac{cos \theta d\theta}{cos(\varphi/2) \sqrt{1-sin^2\theta} }$$

Ну а потом во всех видосах на ютубе с радостным лицом сокращают $cos \theta$ и $ \sqrt{1-sin^2\theta}$
Наверное это будет так если мы работаем с углами до 90, но вопрос, а если у меня маятник был отклонен на 170, и он принимает как острые так и тупые углы, как действовать тогда ?

[Dedekind]

Enceladoglu
Как-то у Вас пределы в интегралах неправильно записаны. Суть в том, что $\theta$ меняется от $-\pi/2$ до $\pi/2$ для любого начального отклонения $\varphi_0$. А значит его косинус всегда положительный.

-- 23.01.2024, 22:38 --

Это видно, если заметить, что $k=\sin\left( \varphi_0/2 \right)$.

[Enceladoglu]

Dedekind
Да, действительно, спасибо.
А вот такой вопрос, ведь углы например $\pi$ и $3\pi$ Это одно и тоже, но мне кажется что тут может возникнуть проблема
P.S ну и да, с пределами интегрирования накосячил когда писал

-- 24.01.2024, 14:37 --

Dedekind
Я имею ввиду, что если мы считаем что после того как маятник совершил полный оборот, мы не начинаем отсчет заново, а продолжаем нагонять фазу
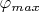
И вероятно, в общем случае$ k = sin \varphi_{max}/2 $, где $\varphi_{max} $максимальный угол отклонения, но эта формула наверное не работает в случае описаном выше

[Dedekind]

Enceladoglu в сообщении #1626989 писал(а):

А вот такой вопрос, ведь углы например $\pi$ и $3\pi$ Это одно и тоже, но мне кажется что тут может возникнуть проблема

Какая, например? Во все формулы углы входят не сами по себе, а в виде аргументов синусов/косинусов. В чем разница между $\sin(\pi)$ и $\sin(3\pi)$?