Всем привет! В учебниках часто вижу примененеие формулы Ньютона-Лейбница вот в такой форме:

Вот пример из учебника Нестерова:

Не могу понять как её вывести?
Пытаюсь вот так: переношу

в левую часть и выношу разность аргументов:
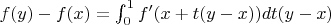
, затем уже интегрирую:

. В итоге получаю некорректное равенство, мешает

, что я делаю не так?