Тогда пусть будет для трех пока
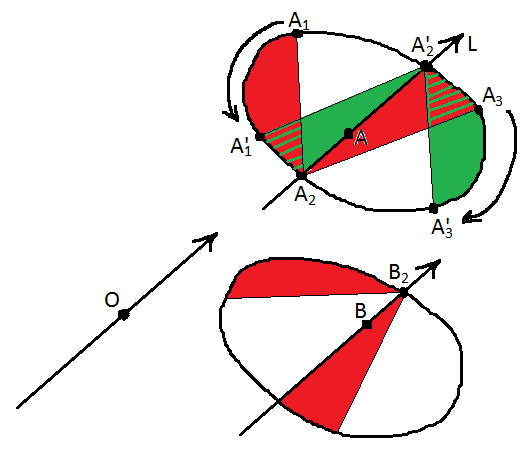
На уровне рукомахательства: Выберем точку

и произвольную прямую, проходящую через эту точку с любым условным направлением. Тогда существует единственная прямая

, параллельная данной, делящая нашу фигуру на две части равной площади. Построим ломаную

как показано на рисунке (площади красных секторов равны шестой части площади фигуры). Начнем движение точки

по прямой

так, чтобы сохранялись площади секторов. Т.о. ломаная

перейдёт в ломаную

а красные сектора перейдут в зелёные. Т.к. движение непрерывно, понятно, что существует точка

такая, что при переходе через неё точки

ломаная превратится в прямую. Аналогично строим точку

(как показано ниже). Если точка

совпала с

то всё доказано, иначе начинаем вращать первоначальную прямую вокруг точки

пока она не совпадет с первоначальной, но с противоположным направлением. Понятно, что при этом точки

и

поменяются местами (Рис. ниже).
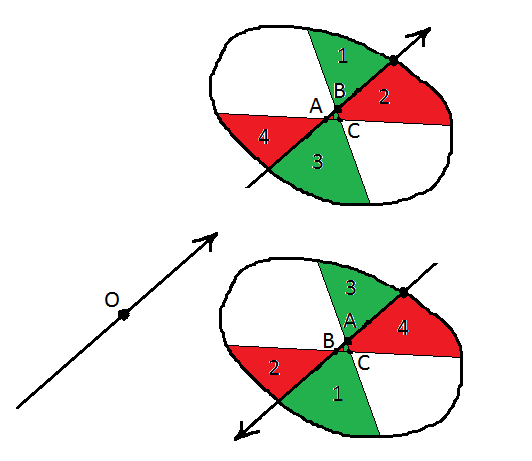
Ну а поскольку вращение непрерывно, и точка

осталась по ту же сторону, что и была (в силу единственности данных трёх прямых), то неизбежна ситуация, когда

совпадёт с

(и еще с

), поскольку, например точка

обязана пересечь прямую

но при этом невозможен случай, чтобы точки

лежали на одной прямой и не совпадали (в этом случае окажутся нулевые площади некоторых сегментов).