По мат.форумам уже давно гуляет следующее доказательство ВТФ.
Рассмотрим уравнение

для случая


Запишем

как

тогда:




Мы получили:

где

- некое натуральное число.
Такое разбиение возможно только если

- составное число и включает в себя
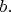
Т.е.

где

- некое натуральное число. Тогда:




Рассмотрим случай, когда

и

взаимно простые.
Тогда

не делится на

. Тогда уравнение

не имеет целочисленного решения.
Тогда рассмотрим обратный случай, когда числа

и

не взаимно простые, и имеют общий делитель.
Тогда

где

- некое натуральное число, уравнение примет вид:


Подытожим. Мы получили:




Подставим эти значения в исходное уравнение:




Очевидно, что это уравнение не имеет решения в целых числах.
Что и требовалось доказать.
-----
Вот такое решение гуляет в интернете. Причем достаточно долго.
Я так понимаю, что где-то ошибка?