Полагаю, все, кто решил не решать эту задачу, давно и успешно её не решили; так что решительно публикую два подхода к её решению.
Подход математическийСделаем два пространственных поворота, установив ось

в направлении точки на сфере, со сферическими координатами
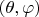
. Матрица перехода получается следующей:
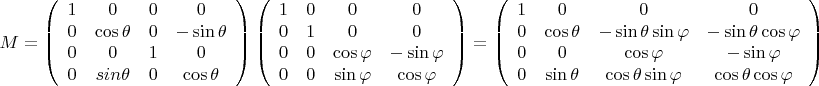
Пусть в штрихованной системе матрица ТЭИ имеет заявленный вид. Тогда в исходной она будет такой:
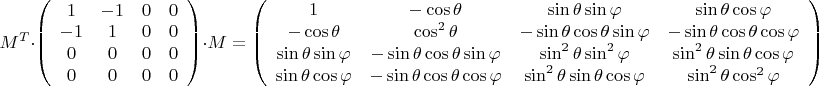
Осредним элементы матрицы по углу

, считая его случайной величиной, равномерно распределённой в интервале
![$[0,2\pi]$ $[0,2\pi]$](https://dxdy-02.korotkov.co.uk/f/5/7/e/57e00d58bd259da9dc7986c73476b95582.png)
. Тогда
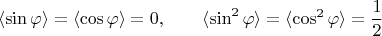
и матрица ТЭИ принимает вид
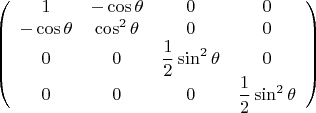
Теперь осредним по углу

, считая его случайной величиной, распределённой на интервале
![$[0,\pi]$ $[0,\pi]$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2385bc03c71e0b4fd8db3bac2e36c7f282.png)
с плотностью
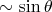
. Тогда
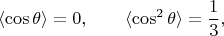
и ответ таков:
 Подход физический
Подход физический В силу симметрии, усреднённый ТЭИ должен иметь вид
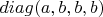
. Причём его след должен быть равен нулю, так как усреднённый ТЭИ линейно накомбинирован из бесследовых тензоров. Следовательно, искомый усреднённый ТЭИ
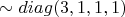
.