Прошу помочь со следующей задачей:
"На единичной сфере произвольно выбираются 4 точки. Найти средний объем тетраэдра с вершинами в этих точках."
Какие у меня есть основные идеи: есть 2 способа векторно задать тетраэдр:
1) задать четыре случайных радиус-вектора

из центра окружности в вершины тетраэдра
2) зафиксировать одну из вершин на сфере и задать три случайных вектора из неё к другим вершинам
3) задать вектор на окружности радиуса

в

(что-то слишком сложное для данной задачи)
При этом я планирую, фиксируя все векторы, кроме одного, усреднять объём по этому вектору, затем усреднять полученное выражение по следующему вектору и т.д. Наиболее удобным мне кажется первый способ, поэтому я распишу его подробнее.
Заметим, что из вершины

выходят три вектора вдоль рёбер тетраэдра:

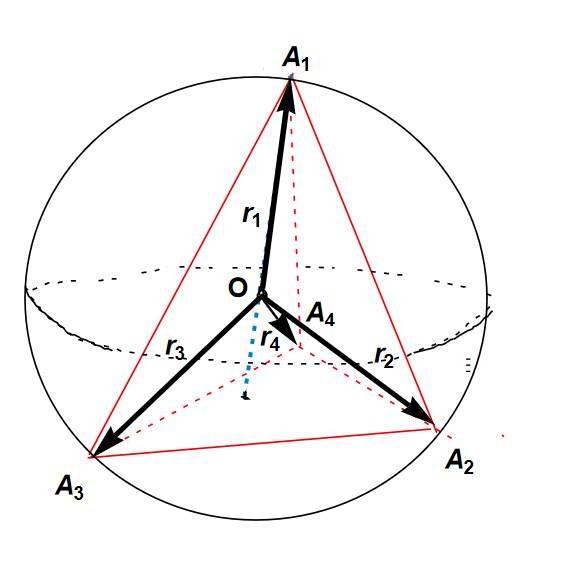
Тогда объём тетраэдра равен:

Проблема, которую я не могу решить - в этом модуле. Если последовательно усреднять моим способом, то непонятно, как раскрывать модуль, и поэтому усреднить выражение я не могу. Аналогичная ситуация вроде бы возникает и во втором способе задания тетраэдра.
Какие ещё методы усреднения тут можно предложить или как избавиться от модуля в моём методе решения?