Модульная арифметика

[Martynov_M]

§1. Определения

В модульной арифметике есть такое понятие как «Порядок числа a по модулю m»:

$a^{\ell} \equiv 1 \pmod m.$
$a, m$ - взаимно простые.

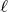
Это выражение известно тем, что $\ell$ делит нацело функцию Эйлера $\varphi(m).$

По теореме Эйлера:
$a^{\varphi(m)} \equiv 1 \pmod m.$

По теореме Лагранжа:
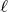
$a^{\ell}$ - образует циклическую подгруппу относительно циклической группы $a^{\varphi(m)}$, и поэтому $\ell$ делит нацело $\varphi(m).$

Пример.
Сравним $9^{n}$ по модулю 17:

$9^{1} \equiv 9 \; \, \pmod {17}.$
$9^{2} \equiv 13 \pmod {17}.$
$9^{3} \equiv 15 \pmod {17}.$
$9^{4} \equiv 16 \pmod {17}.$
$9^{5} \equiv 8 \; \, \pmod {17}.$
$9^{6} \equiv 4 \; \, \pmod {17}.$
$9^{7} \equiv 2 \; \, \pmod {17}.$
$9^{8} \equiv 1 \; \, \pmod {17}.$

Мы получили группу вычетов из 8 элементов: {9, 13, 15, 16, 8, 4, 2, 1}.

По теореме Эйлера:

$a^{\varphi(m)} \equiv 1 \pmod m.$

$9^{\varphi(17)} \equiv 1 \pmod {17}.$

$9^{16} \equiv 1 \pmod {17}.$

Тогда продолжим возводить в степень $9^{n}$ и далее:

$9^{9} \; \, \equiv 9 \; \, \pmod {17}.$
$9^{10} \equiv 13 \pmod {17}.$
$9^{11} \equiv 15 \pmod {17}.$
$9^{12} \equiv 16 \pmod {17}.$
$9^{13} \equiv 8 \; \, \pmod {17}.$
$9^{14} \equiv 4 \; \, \pmod {17}.$
$9^{15} \equiv 2 \; \, \pmod {17}.$
$9^{16} \equiv 1 \; \, \pmod {17}.$

Мы получили группу вычетов из 16 элементов: {9, 13, 15, 16, 8, 4, 2, 1, 9, 13, 15, 16, 8, 4, 2, 1}.

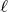
Циклическая группа $9^{8}$ является подгруппой циклической группы $9^{16}$ и поэтому $\ell$ делит нацело $\varphi(m).$
16 / 8 = 2.

Но остается вопрос, почему вообще прогрессия $a^{n}$ образует циклическую группу?

§2. Периодичность остатков при возведении в степень.

Докажем, что при любых натуральных $a, m$ остатки от деления $a^{1}, a^{2}, a^{3}, a^{4}, a^{5},\ldots$ на $m$ периодически повторяются.
Для этого рассмотрим первые $m+1$ степеней:

$a^{1}, a^{2}, a^{3}, \ldots, a^{m}, a^{m+1}.$

При делении на $m$ может быть только $m$ остатков $(0, 1, 2, \ldots, m-1)$. Но чисел у нас $m+1$. Это значит, что среди них найдется хотя бы два таких числа, имеющих одинаковые остатки:

$a^{k_{1}} \equiv x \pmod {m}.$
$a^{k_{2}} \equiv x \pmod {m}.$

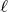
Пусть $k_{2} > k_{1},$ тогда $k_{2} = k_{1}+\ell$, где $\ell$ – некое натуральное число. Тогда:

$a^{k_{1}} \; \; \; \; \! \equiv x \pmod {m}.$
$a^{k_{1}+\ell} \equiv x \pmod {m}.$

Следовательно:

$a^{k_{1}} \equiv a^{k_{1}+\ell} \pmod {m}.$

Умножим последнее равенство на $a^{n - k_{1}},$ где $n$ - произвольное число, $n \geq k_{1}.$ Получим:

$a^{n} \equiv a^{n+\ell} \pmod {m}.$

Это означает, что начиная с некоторой степени $a^{k_{1}}$ остатки периодически повторяются. И их период равен $\ell$.

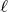
§3. Периодичность остатков, когда a, m - взаимно простые.

Еще проще обнаружить периодичность остатков $a^{1}, a^{2}, a^{3}, a^{4}, a^{5},\ldots$, для случая, когда $a, m$ - взаимно простые.
По теореме Эйлера:

$a^{\varphi(m)} \equiv 1 \pmod m.$
$a^{\ell} \quad \quad \! \! \! \equiv 1 \pmod m.$

Умножим обе части этого сравнения на произвольную степень $a^{n}:$

$a^{n+\ell} \equiv a^{n} \pmod {m}.$

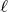
Остатки повторяются с периодом $\ell$, начиная с самой первой степени:

$a^{1+\ell} \equiv a^{1} \pmod {m}.$

Это была теоретическая основа. Теперь по существу.

Задача

Есть уравнение:

$y = \dfrac{2^{k}n - 1}{m}$

где $k$ – натуральное.
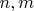
$n, m$ – нечетные: 1, 3, 5, 7, 9…

Докажите возможность существования целочисленного решения $\dfrac{2^{k}n - 1}{m}$ относительно:
$n \equiv 1 \pmod m.$
$n \equiv 2 \pmod m.$
$n \equiv 3 \pmod m.$
$n \equiv \ldots \pmod m.$
$n \equiv m - 1 \pmod m.$

Запишем $n$ в виде:

$n = zm + x,$ где $x$ – это вычеты по модулю $m$.
$x$ - принимает значения от 1 до $m-1.$

Тогда уравнение $y$ примет вид:

$y = \dfrac{2^{k}n - 1}{m} = \dfrac{2^{k}(zm + x) - 1}{m} = \dfrac{2^{k}zm + 2^{k}x - 1}{m} = \dfrac{2^{k}zm}{m} + \dfrac{2^{k}x - 1}{m} = 2^{k}z + \dfrac{2^{k} x - 1}{m}.$

Таким образом, мы сузили область поиска целочисленных решений $y$ относительно вычетов $x$ до области поиска целочисленных решений:

$\dfrac{2^{k} x - 1}{m},$ где $x$ принимает значения от 1 до $m-1.$

Запишем это уравнение в виде:

$2^{k} x - 1 \equiv 0 \pmod m.$

$2^{k} x \equiv 1 \pmod m.$

По правилам модульной арифметики это уравнение всегда имеет решение при любых значениях параметров $k, m$, потому что $2^{k}$ и $m$ - взаимно простые.
Таким образом, задача решена.

Примеры.

$m$ = 3. Решение: $y = \begin{cases} \frac{2n-1}{3}, & n \equiv 2 \pmod 3 \\ \frac{4n-1}{3}, & n \equiv 1 \pmod 3 \end{cases}$

$m$ = 5. Решение: $y = \begin{cases} \frac{2n-1}{5}, & n \equiv 3 \pmod 5 \\ \frac{4n-1}{5}, & n \equiv 4 \pmod 5 \\ \frac{8n-1}{5}, & n \equiv 2 \pmod 5 \\ \frac{16n-1}{5}, & n \equiv 1 \pmod 5 \end{cases}$

$m$ = 7. Решение: $y = \begin{cases} \frac{2n-1}{7}, & n \equiv 4 \pmod 7 \\ \frac{4n-1}{7}, & n \equiv 2 \pmod 7 \\ \frac{8n-1}{7}, & n \equiv 1 \pmod 7 \end{cases}$

$m$ = 9. Решение: $y = \begin{cases} \frac{2n-1}{9}, & n \equiv 5 \pmod 9 \\ \frac{4n-1}{9}, & n \equiv 7 \pmod 9 \\ \frac{8n-1}{9}, & n \equiv 8 \pmod 9 \\ \frac{16n-1}{9}, & n \equiv 4 \pmod 9 \\ \frac{32n-1}{9}, & n \equiv 2 \pmod 9 \\ \frac{64n-1}{9}, & n \equiv 1 \pmod 9 \end{cases}$

$m$ = 11. Решение: $y = \begin{cases} \frac{2n-1}{11}, & n \equiv 6 \pmod {11} \\ \frac{4n-1}{11}, & n \equiv 3 \pmod {11} \\ \frac{8n-1}{11}, & n \equiv 7 \pmod {11} \\ \frac{16n-1}{11}, & n \equiv 9 \pmod {11} \\ \frac{32n-1}{11}, & n \equiv 10 \pmod {11}\\ \frac{64n-1}{11}, & n \equiv 5 \pmod {11}\\ \frac{128n-1}{11}, & n \equiv 8 \pmod {11}\\ \frac{256n-1}{11}, & n \equiv 4 \pmod {11}\\ \frac{512n-1}{11}, & n \equiv 2 \pmod {11}\\ \frac{1024n-1}{11}, & n \equiv 1 \pmod {11}\end{cases}$

Задача №2.

Докажите, что $n \equiv 1 \pmod m$ всегда имеет максимальную степень двойки $2^{k}$ в задаче №1.

Перейдем к уравнению:

$2^{k} x - 1 \equiv 0 \pmod m.$

$2^{k} x \equiv 1 \pmod m.$

где $x$ - это вычеты от 1 до $m - 1.$
Нужно доказать, что $x=1$ имеет максимальную степень двойки $2^{k}$. Докажем это.

Доказательство.
Обозначим степень, которая соответствует значению $x=1$ как $\ell$,

$2^{\ell} \cdot 1 \, \equiv 1 \pmod m.$

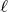
Теперь рассмотрим следующие сравнения:

$2^{\ell} \cdot 1 \, \equiv 1 \pmod m.$
$2^{k} \cdot x \equiv 1 \pmod m.$

В первом $x=1$, а во втором $x \neq 1.$
Попарно перемножим их:

$2^{k +\ell} \cdot x \equiv 1 \pmod m.$

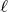
Это означает, что любое решение $x$ повторяется с периодом $\ell$, начиная с самого первого решения.
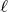
$\ell$ – максимальное число в периоде. $2^{\ell}$ - максимальная степень двойки.
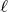
$\ell$ – можно получить только при $x=1$. Что и требовалось доказать.

Конец статьи.
---

В общем, интересует математическая строгость текста.
Не наделал ли я во всех этих суждениях ошибок?

Акцент на том, что $x=1$ дает максимальную степень двойки. И надо это доказать.