Поскольку арифметическая функция является функцией натурального аргумента, то для нее можно использовать некоторые определения и утверждения из области почти периодических функций.
Определение 1. Арифметическая функция

называется почти периодической в смысле Бора, если для любого
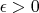
существует такое натуральное

, что любой отрезок
![$[a,a+l]$ $[a,a+l]$](https://dxdy-03.korotkov.co.uk/f/6/d/5/6d576ccba37160adb28be51f392d94fd82.png)
(

- любое натуральное число) содержит по меньшей мере одно натуральное

, для которого выполняется:

.
Утверждение 1. Для каждой почти периодической арифметической функции в смысле Бора

существует конечный предел среднего значения:
![$\lim_{n \to \infty} {E[f,n]} =\lim_{n \to \infty} \frac {1}{n}\sum_{m \leq n}{f(m)}$ $\lim_{n \to \infty} {E[f,n]} =\lim_{n \to \infty} \frac {1}{n}\sum_{m \leq n}{f(m)}$](https://dxdy-01.korotkov.co.uk/f/4/9/5/495a5b330327d3112b25b3e8ce02589c82.png)
.
Определение 2. Арифметическая функция

является периодической с периодом

, отличным от нуля,, если для каждого натурального значения

выполняется

.
Например, периодической c

является арифметическая функция

.
Таким образом, периодическая арифметическая функция является частным случаем почти периодической арифметической функции в смысле Бора. Поэтому для периодической арифметической функции справедливо утверждение 1, т.е. существует конечный предел ее среднего значения, который определяется следующим утверждением.
Утверждение 2. Предел среднего значения периодической арифметической функции

равен:
![$\lim_{n \to \infty} {E[f,n]} =\lim_{n \to \infty} \frac {1}{n}\sum_{m \leq n}{f(m)}=\frac {1}{T}\sum_{m \leq T}{f(m)}$ $\lim_{n \to \infty} {E[f,n]} =\lim_{n \to \infty} \frac {1}{n}\sum_{m \leq n}{f(m)}=\frac {1}{T}\sum_{m \leq T}{f(m)}$](https://dxdy-02.korotkov.co.uk/f/d/f/a/dfa7ef03ade542f32039a707b5f5a14382.png)
,
где

(отличен от нуля) - период арифметической функции

.
Думаю, что они справедливы. Если нет, то прошу менять поправить.