Задача из учебника Беклемишева

[Verbery]

Всем привет! Задача #3, главы 1, параграфа 4. Я не могу её дорешать до конца, моё решение получается с углом $\varphi$ и не знаю как от него избавиться. Вот условие:
"Найдите сумму векторных проекций вектора $a$ на стороны заданного правильного треугольника"

Пытаюсь решать так. Обозначим треугольник из условия как $ABC$. Отложим на каждой стороне свой еденичный отрезок: $e_1$, $e_2$, $e_3$. Найдём длину каждой проекции, для этого воспользуемся известной формулой для подсчёта координаты проекции на прямой:
$Pr AC = \frac{(\vec{a}, e_i)}{|e_i|}$, где $e_i$ - базисный вектор коллинеарный стороне прямоугольника, на которую проектируется вектор. Базис возьмём ортонормированный, поэтому длина каждой проекции будет равна $(a,\vec{e_i})$. Поэтому длина всех проекций равна: $(a, \vec{e_1}) + (a, \vec{e_2}) + (a, \vec{e_3}) = (a, \vec{e_1} + \vec{e_2} + \vec{e_3})$ далее воспользовавшись тем, что каждый единичный вектор $e_i$ лежит на стороне правильного треугольника преобразуем сумму и получим: $(a, 3 \vec{e_2})=3(a, \vec{e_2})=3 a \cos{\varphi}$, где $\varphi$ - это угол между $e_2$ и $a$

Вопрос а что дальше можно было бы сделать с формулой $3 a \cos{\varphi}$ или я пошёл вообще не в ту сторону?

[Geen]

Verbery в сообщении #1601886 писал(а):

базисный вектор коллинеарный стороне прямоугольника

Verbery в сообщении #1601886 писал(а):

Базис возьмём ортонормированный

это как?

[Verbery]

Geen в сообщении #1601888 писал(а):

Verbery в сообщении #1601886 писал(а):

базисный вектор коллинеарный стороне прямоугольника

Verbery в сообщении #1601886 писал(а):

Базис возьмём ортонормированный

это как?

Всмысле я для каждой стороны строю свой ортонормированный базис

[Dedekind]

Verbery в сообщении #1601886 писал(а):

Обозначим треугольник из условия как $ABC$. Отложим на каждой стороне свой еденичный отрезок: $e_1$, $e_2$, $e_3$. Найдём длину каждой проекции, для этого воспользуемся известной формулой для подсчёта координаты проекции на прямой:
$Pr AC = \frac{(\vec{a}, e_i)}{|e_i|}$, где $e_i$ - базисный вектор коллинеарный стороне прямоугольника, на которую проектируется вектор.

А три вектора на сторонах треугольника образуют базис?

Verbery в сообщении #1601886 писал(а):

Вопрос а что дальше можно было бы сделать с формулой $3 a \cos{\varphi}$ или я пошёл вообще не в ту сторону?

Очевидно же, что не в ту. По этой формуле, если вектор $a$ ортогонален $e_2$, то сумма проекций равна 0. А на самом деле?

[Verbery]

Dedekind в сообщении #1601897 писал(а):

А три вектора на сторонах треугольника образуют базис?

Нет, для каждой стороны составляем свой базис, в котором сторона коллинеарна базисному вектору. Потом находим длину проекции для каждого базиса и суммируем их. А направление найдём из суммирования единичных векторов на сторонах правильного треугольника

[svv]

Расположите треугольник, как на левой картинке. Разложите вектор $\mathbf a$ на вертикальную $\mathbf v$ и горизонтальную $\mathbf h$ составляющую. Изучите, что делает с каждой из составляющих операция "заменим вектор суммой его векторных проекций на все стороны треугольника" (без базисов, только школьная геометрия на уровне знания $\cos 30°$). Окажется, что эта операция просто растягивает и $\mathbf v$, и $\mathbf h$ в $k_v$ и $k_h$ раз соответственно, а направление сохраняет. Найдите $k_v$ и $k_h$. Они равны или нет?

На правой картинке показан вектор $\mathbf v$ и его векторные проекции на две зелёные стороны (а на красную нулевая). Сумма проекций не показана, но ясно, что она направлена вертикально.

[мат-ламер]

Verbery в сообщении #1601886 писал(а):

моё решение получается с углом $\varphi$ и не знаю как от него избавиться.

Verbery в сообщении #1601886 писал(а):

Вопрос а что дальше можно было бы сделать с формулой $3 a \cos{\varphi}$ или я пошёл вообще не в ту сторону?

Мне кажется, раскрывать скалярное произведение через угол тут не стоит. Интуиция подсказывает, что в итоге там должно кое-что сократиться, учитывая, чему равна сумма $\vec{e_i}$ .

[Verbery]

svv

Я так понял ваша идея состоит в том, что проекция вектора $\vec{a}$ на красную сторону будет равна $k_h h$, а вот с проекцией $v$ на зелёные стороны я не могу разобраться. Ведь проекция $\vec{a}$ на зелёные стороны не равна проекции $\vec{v}$ на зелёные стороны. Если же выражаю через косинусы, то у меня опять вылазит там угол $\varphi$, который нам неизвестен. Где там линейность я тоже не увидел, не могу увязать вектор $v$ с проекцией вектора $a$ на зелёные стороны треугольника

[svv]

Verbery
В учебнике даётся, чуть в иных обозначениях, такая формула (11, с.33):
$\operatorname{pr}_{\mathbf e}\mathbf a=\frac{(\mathbf a, \mathbf e)}{(\mathbf e, \mathbf e)}\mathbf e$
Здесь $\mathbf e$ в левой части — ненулевой вектор, определяющий семейство параллельных ему прямых (фактически, вектор, на который проектируем). Результат проектирования
$\bullet$ не зависит от того, какая прямая из этого семейства выбрана, и
$\bullet$ не изменится, если $\mathbf e$ растянуть в $k\neq 0$ раз ($k$ может быть и отрицательным, что соответствует противоположному направлению).

Из формулы видно, что $\operatorname{pr}_{\mathbf e}\mathbf a$ линейно по $\mathbf a$, то есть если $\mathbf a=\mathbf v+\mathbf h$, то
$\operatorname{pr}_{\mathbf e}\mathbf a=\operatorname{pr}_{\mathbf e}\mathbf v+\operatorname{pr}_{\mathbf e}\mathbf h$
Каждое из слагаемых в правой части несложно вычисляется для каждой из сторон. Векторы, параллельные зелёным сторонам, обозначим $\mathbf e_1, \mathbf e_2$, а вектор красной стороны обозначим $\mathbf e_3$.

Найдём сумму векторных проекций $\mathbf v$ на все три стороны. Ясно, что проекция $\mathbf v$ на красную сторону равна нулю.

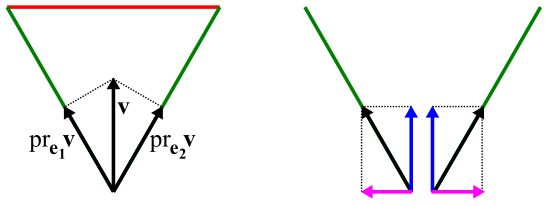
Остаётся найти сумму проекций $\mathbf v$ на зелёные стороны (левая картинка).
Начнём с того, что длина каждой из них составляет $|\mathbf v|\cos 30°$: каждая проекция — катет, прилежащий углу $30°$, а вертикальная гипотенуза равна $|\mathbf v|$.
Каждую из двух проекций можно опять разложить на вертикальную и горизонтальную составляющую (правая картинка). Горизонтальные составляющие (малиновые) уничтожают друг друга, остаются вертикальные (синие). Длина каждого синего вектора равна $|\mathbf v|\cos^2 30°=\frac 3 4 |\mathbf v|$. Поскольку синие сонаправлены $\mathbf v$, каждый синий равен $\frac 3 4 \mathbf v$, и
$\operatorname{pr}_{\mathbf e_1}\mathbf v +\operatorname{pr}_{\mathbf e_2}\mathbf v = \frac 3 2\mathbf v$

Пожалуйста, рассмотрите аналогично проекции $\mathbf h$. Там уже будут работать все три стороны. Каждую проекцию опять можно разложить на верт. и гор. составляющие, что-то уничтожится, что-то, наоборот, удвоится...

[мат-ламер]

Verbery в сообщении #1601886 писал(а):

Базис возьмём ортонормированный, поэтому длина каждой проекции будет равна $(a,\vec{e_i})$. Поэтому длина всех проекций равна: $(a, \vec{e_1}) + (a, \vec{e_2}) + (a, \vec{e_3}) = (a, \vec{e_1} + \vec{e_2} + \vec{e_3})$

Если векторы складываются, то их длины при этом не складываются. У меня подозрение, что вы теорию не до конца освоили. Однако, не буду вмешиваться. Может я не так понял вашу мысль.

И, вообще, что такое "длина всех проекций"? Вместо этого ищите сразу векторную сумму всех проекций.

[TOTAL]

Verbery в сообщении #1601886 писал(а):

или я пошёл вообще не в ту сторону?

Попробуйте вот в эту сторону сходить.
1. Пусть вектор параллелен стороне треугольника. Какой ответ? (Изменилось ли направление исходного вектора? Как изменилась длина?)
2. Любой вектор можно представить в виде суммы двух векторов, каждый из которых параллелен стороне треугольника.
3. Ответ для суммы равен сумме ответов.

[мат-ламер]

Verbery в сообщении #1601886 писал(а):

Базис возьмём ортонормированный, поэтому длина каждой проекции будет равна $(a,\vec{e_i})$. Поэтому длина всех проекций равна: $(a, \vec{e_1}) + (a, \vec{e_2}) + (a, \vec{e_3}) = (a, \vec{e_1} + \vec{e_2} + \vec{e_3})$

Позвольте немного отредактировать мысль:

Verbery в сообщении #1601886 писал(а):

Базис возьмём ортонормированный, поэтому длина каждой проекции будет равна $(a,\vec{e_i})$. Поэтому сумма всех проекций равна вектору: $(a, \vec{e_1})\vec{e_1} + (a, \vec{e_2})\vec{e_2} + (a, \vec{e_3})\vec{e_3} = ...$

.
Последнее слагаемое можно раскрыть. Кое-что подсократится. А можно и не раскрывать. Угол в скалярном произведении вытаскивать не надо.

[Verbery]

svv в сообщении #1602315 писал(а):

Пожалуйста, рассмотрите аналогично проекции $\mathbf h$. Там уже будут работать все три стороны. Каждую проекцию опять можно разложить на верт. и гор. составляющие, что-то уничтожится, что-то, наоборот, удвоится...

Вроде проблем с заменой $\vec{a}$ на сумму проекций на треугольник не возникало, у меня получилась вот такая сумма проекций, если идти по вашему способу решения: $\vec{s} = \frac{3}{4} k_v \vec{v} + 3 k_h \vec{h}$. Но вот как найти $k_v$ и $k_h$ я что-то не пойму. Нашёл непосредственно через косинус и синус: $\frac{3}{4} k_v \vec{v} + 3 k_h \vec{h} = \frac{3}{4} |\vec{a}| \cos{\varphi} + 3 |\vec{a}| \cos({\frac{\pi}{2} - \varphi}) = \frac{3}{4} |\vec{a}| \cos{\varphi} + 3 |\vec{a}| \sin{\varphi}$, но угол $\varphi$ неизвестен. Я совсем элементарных вещей видимо не вижу?

[svv]

svv в сообщении #1602315 писал(а):

каждый синий равен $\frac 3 4 \mathbf v$

Но синих-то два. Поэтому $\frac 3 2\mathbf v$ (я об этом писал).
И вот этот коэффициент $\frac 3 2$ и есть $k_v$. Мы нашли $k_v$, и он равен $\frac 3 2$.

Если теперь аккуратно найти $k_h$, окажется, что он тоже равен $\frac 3 2$. А потому весь вектор $\mathbf v$ операцией "заменить вектор на сумму его векторных проекций на все стороны" просто умножается на $\frac 3 2$, и никакой угловой зависимости в итоге нет.

[Verbery]

svv

Спасибо, вроде разобрался. В итоге ответ будет такой: сумма векторных проекций направлена под углом 45 градусов к оси $h$ в ортонормированном базисе $h$ и $v$, а длина её будет больше в $\frac{3}{2}$ раза каждого базисного вектора, из которого состоит $\vec{a}$