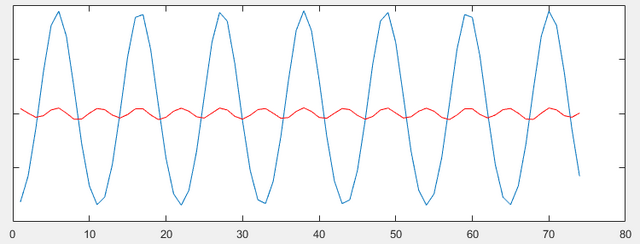
B@R5ukЯ посмотрел ваш код и решил похожим образом "спасти" свой. Вроде сделал то же самое, но таких отличных результатов не получил. Вот код для одной гармоники:
Код:
B_COEF=fminbnd(@LS1, a_n, b_n); @a_n и b_n – начальные приближения, которые точно выбраны верно
A=[ones(size(y,1),1), cos(2*pi*B_COEF*x), sin(2*pi*B_COEF*x)];
COEFS=pinv(A)*y
function S = LS1(b)
y=[61.8345252303583; 64.2186685630058; 68.5780907223303; 73.8351943469310; ...
78.1178746381488; 79.4447599032848; 77.1209584326325; 72.3384843492439; ...
67.1780874592201; 63.3083342155163; 61.5848686426315; 62.2811015529467; ...
65.2944676251564; 70.0570903999628; 75.2539157928855; 78.8647097424086; ...
79.1332309482167; 75.9175990711235; 70.8145100998371; 65.8890541188997; ...
62.5767534515232; 61.5348068381206; 62.9195242022718; 66.5179434492526; ...
71.5768723085928; 76.5420755341518; 79.3273502810222; 78.5249447120497; ...
74.5575769012328; 69.3099594259272; 64.7368823911916; 62.0334551154671; ...
61.6848623894562; 63.7418912006921; 67.8660696583989; 73.0933449460809; ...
77.6481344114599; 79.4840538567364; 77.6481344114599; 73.0933449460811; ...
67.8660696583989; 63.7418912006923; 61.6848623894562; 62.0334551154669; ...
64.7368823911916; 69.3099594259272; 74.5575769012327; 78.5249447120497; ...
79.3273502810222; 76.5420755341517; 71.5768723085929; 66.5179434492527; ...
62.9195242022719; 61.5348068381207; 62.5767534515231; 65.8890541188995; ...
70.8145100998372; 75.9175990711235; 79.1332309482166; 78.8647097424087; ...
75.2539157928858; 70.0570903999627; 65.2944676251561; 62.2811015529469; ...
61.5848686426318; 63.3083342155164; 67.1780874592199; 72.3384843492438; ...
77.1209584326324; 79.4447599032847; 78.1178746381488; 73.8351943469311; ...
68.5780907223305; 64.2186685630060 ];
n=size(y,1);
x=(1:n)';
A=[ones(size(y,1),1), cos(2*pi*b*x), sin(2*pi*b*x)];
c=pinv(A)*y;
S=norm(y-A*c);
end
Получаем следующее:
Код:
COEFS =
69.997493484633836
-8.559819480269374
-2.657659629898907
Хорошо, добавим ещё одну гармонику:
Код:
B_COEF2=fminbnd(@LS2, a_n, b_n)
A2=[ones(size(y,1),1), cos(2*pi*B_COEF2*x), sin(2*pi*B_COEF2*x),...
cos(2*pi*B_COEF2*x*2), sin(2*pi*B_COEF2*x*2)];
COEFS2=pinv(A2)*y
function S = LS2(b)
y=[61.8345252303583; 64.2186685630058; 68.5780907223303; 73.8351943469310; ...
78.1178746381488; 79.4447599032848; 77.1209584326325; 72.3384843492439; ...
67.1780874592201; 63.3083342155163; 61.5848686426315; 62.2811015529467; ...
65.2944676251564; 70.0570903999628; 75.2539157928855; 78.8647097424086; ...
79.1332309482167; 75.9175990711235; 70.8145100998371; 65.8890541188997; ...
62.5767534515232; 61.5348068381206; 62.9195242022718; 66.5179434492526; ...
71.5768723085928; 76.5420755341518; 79.3273502810222; 78.5249447120497; ...
74.5575769012328; 69.3099594259272; 64.7368823911916; 62.0334551154671; ...
61.6848623894562; 63.7418912006921; 67.8660696583989; 73.0933449460809; ...
77.6481344114599; 79.4840538567364; 77.6481344114599; 73.0933449460811; ...
67.8660696583989; 63.7418912006923; 61.6848623894562; 62.0334551154669; ...
64.7368823911916; 69.3099594259272; 74.5575769012327; 78.5249447120497; ...
79.3273502810222; 76.5420755341517; 71.5768723085929; 66.5179434492527; ...
62.9195242022719; 61.5348068381207; 62.5767534515231; 65.8890541188995; ...
70.8145100998372; 75.9175990711235; 79.1332309482166; 78.8647097424087; ...
75.2539157928858; 70.0570903999627; 65.2944676251561; 62.2811015529469; ...
61.5848686426318; 63.3083342155164; 67.1780874592199; 72.3384843492438; ...
77.1209584326324; 79.4447599032847; 78.1178746381488; 73.8351943469311; ...
68.5780907223305; 64.2186685630060 ];
n=size(y,1);
x=(1:n)';
A=[ones(size(y,1),1), cos(2*pi*b*x), sin(2*pi*b*x), cos(2*pi*b*x*2), sin(2*pi*b*x*2)];
c=pinv(A)*y;
S=norm(y-A*c);
end
Получим следующее:
Код:
COEFS2 =
69.999382251747747
-8.577036036723200
-2.568021866649669
0.423315666248895
0.278063775718108
Точность повысилась (напомню, что постоянная составляющая в идеальном случае должна равняться 70). Добавим третью гармонику:
Код:
B_COEF3=fminbnd(@LS3, a_n, b_n)
A3=[ones(size(y,1),1), cos(2*pi*B_COEF3*x), sin(2*pi*B_COEF3*x), ...
cos(2*pi*B_COEF3*x*2), sin(2*pi*B_COEF3*x*2), cos(2*pi*B_COEF3*x*3), sin(2*pi*B_COEF3*x*3)];
COEFS3=pinv(A3)*y
function S = LS3(b)
y=[61.8345252303583; 64.2186685630058; 68.5780907223303; 73.8351943469310; ...
78.1178746381488; 79.4447599032848; 77.1209584326325; 72.3384843492439; ...
67.1780874592201; 63.3083342155163; 61.5848686426315; 62.2811015529467; ...
65.2944676251564; 70.0570903999628; 75.2539157928855; 78.8647097424086; ...
79.1332309482167; 75.9175990711235; 70.8145100998371; 65.8890541188997; ...
62.5767534515232; 61.5348068381206; 62.9195242022718; 66.5179434492526; ...
71.5768723085928; 76.5420755341518; 79.3273502810222; 78.5249447120497; ...
74.5575769012328; 69.3099594259272; 64.7368823911916; 62.0334551154671; ...
61.6848623894562; 63.7418912006921; 67.8660696583989; 73.0933449460809; ...
77.6481344114599; 79.4840538567364; 77.6481344114599; 73.0933449460811; ...
67.8660696583989; 63.7418912006923; 61.6848623894562; 62.0334551154669; ...
64.7368823911916; 69.3099594259272; 74.5575769012327; 78.5249447120497; ...
79.3273502810222; 76.5420755341517; 71.5768723085929; 66.5179434492527; ...
62.9195242022719; 61.5348068381207; 62.5767534515231; 65.8890541188995; ...
70.8145100998372; 75.9175990711235; 79.1332309482166; 78.8647097424087; ...
75.2539157928858; 70.0570903999627; 65.2944676251561; 62.2811015529469; ...
61.5848686426318; 63.3083342155164; 67.1780874592199; 72.3384843492438; ...
77.1209584326324; 79.4447599032847; 78.1178746381488; 73.8351943469311; ...
68.5780907223305; 64.2186685630060 ];
n=size(y,1);
x=(1:n)';
A=[ones(size(y,1),1), cos(2*pi*b*x), sin(2*pi*b*x), cos(2*pi*b*x*2), sin(2*pi*b*x*2), ...
cos(2*pi*b*x*3), sin(2*pi*b*x*3)];
c=pinv(A)*y;
S=norm(y-A*c);
end
Получим вывод:
Код:
COEFS3 =
69.999189367018261
-8.577273863261093
-2.568672462247298
0.422812571305099
0.278117683581578
-0.015454583668819
-0.018555204536330
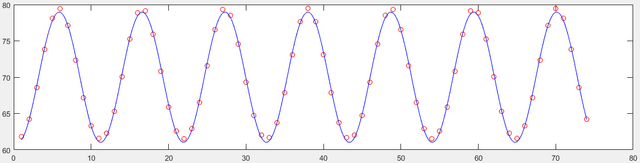
Результат изменился, но не в нашу пользу. Не понимаю, почему такое происходит. Также не очень ясно, какой вы в своём графике (где синусоида проходит точно по точкам) выводите сигнал. Если полигармонический, то я не понимаю, как такое возможно – у меня выходит совсем не синусоида. Если просто используете основную гармонику, то тоже не очень ясно. Изначально отклонение от идеальной постоянной составляющей было 3 тысячных. У вас, конечно, в тысячи раз меньше получилось, но ведь на графике, который был приведён
svv, видно, что синусоиду нужно сдвинуть где-то на 0.5


 , то найденный коэффициент
, то найденный коэффициент  невязки
невязки  . В этой точке
. В этой точке  . Поэтому в малой окрестности точки
. Поэтому в малой окрестности точки  справедливо приближение
справедливо приближение
 равны
равны

 .
.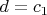 ), чтобы уменьшить невязку?
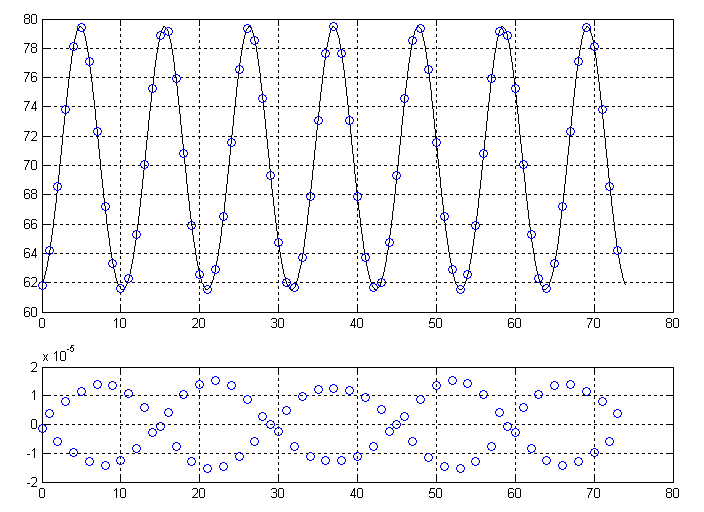
), чтобы уменьшить невязку? присутствует довольно заметная вторая гармоника. И её фаза такова, что её максимумы совпадают с максимумами и минимумами основной синусоиды, а её минимумы приходятся на "склоны" основной синусоиды. А на склонах разница мало заметна на графике. Вот и кажется, что синусоиду стоило бы подвинуть вверх.
присутствует довольно заметная вторая гармоника. И её фаза такова, что её максимумы совпадают с максимумами и минимумами основной синусоиды, а её минимумы приходятся на "склоны" основной синусоиды. А на склонах разница мало заметна на графике. Вот и кажется, что синусоиду стоило бы подвинуть вверх. ). Постоянные составляющие выброшены. Видно, что львиная доля остатка приходится на вторую гармонику.
). Постоянные составляющие выброшены. Видно, что львиная доля остатка приходится на вторую гармонику.