Помогите пожалуйста решить или дайте легкую подсказку:
Нужно доказать, что
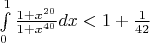
Первое, что приходит в голову, попытаться доказать, что подынтегральное выражение на отрезке от 0 до 1 меньше, чем

, и дальше проинтегрировать обе части. Но это не так. Какой-то стандартный трюк видимо есть, который не могу найти.