Почему равен нулю потенциал на хорде.
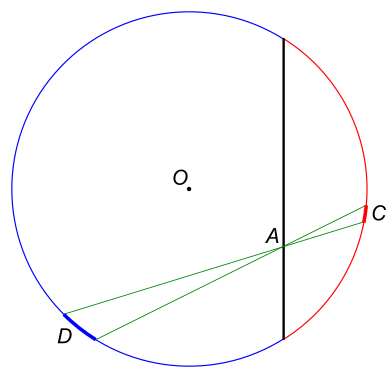
Хорда разбивает окружность на две дуги, заряженные положительно (красная) и отрицательно (синяя). Возьмём на хорде точку

. Проведём через неё две прямых с очень малым углом между ними. Прямые вырезают на окружности две маленькие дужки (жирная красная и жирная синяя). Так как угол мал, расстояние от

до любой точки красной дужки

, а до любой точки синей дужки

, где

и

— некоторые точки на дужках. Малые длины дужек (а следовательно, и их заряды по абсолютной величине) относятся как

. Поэтому вклады дужек в потенциал компенсируются.
-- Ср фев 01, 2023 01:22:49 --Почему равен нулю потенциал на дуге окружности, полученной инверсией хорды.
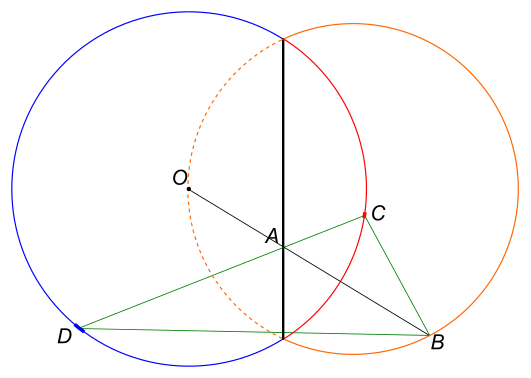
Инверсия прямой, на которой лежит хорда, относительно "заряженной" окружности, даёт окружность (оранжевую), проходящую через

и концы хорды. Инверсия только самой хорды даёт сплошную дугу оранжевой окружности — т.е. её внешнюю часть по отношению к "заряженной" окружности.
Возьмём ту же точку

на хорде и те же малые дужки

и

. Построим точку

инверсией точки

.
"Заряженная" окружность является
окружностью Аполлония для точек

и

, то есть для любых двух точек

и

на ней

.
Поэтому вклады дужек в потенциал в точке

также компенсируются (заряды те же, а расстояния в

раз больше).