У меня два решения получилось:
(Оффтоп)
Пусть

- рациональное
Тогда

Пусть

- целые, и

Перепишем:

Получаем, что

- Пифагорова тройка
То есть



Мы не рассматриваем только примитивные тройки, поэтому ограничений на
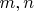
не накладываем, кроме целости, и обозначим

- рациональное, кроме того, далее учтем возможную потерю знака у решения от возведения квадрат.
Заметим, что


Поэтому ищем

из выражений


Первое дает

Второе:

В силу рациональности

можем отбросить в обеих формулах знак "плюс-минус", и останется ответ.

(Это то же самое, только со сдвигом на 3)
