So I expect the PARI code to check

, for some computed maximum.
But no one forbids checking not

, but this much

.
If "qrmin" is correctly calculated as the minimum valid

, then "sqrt(stop/qrmin)" seems like the correct way to get the computed maximum, but when I talk about "pmin" I'm talking about that value Z. If you're going to calculate it from qrmax, it would probably be "sqrt(stop/qrmax)", but that calculation also does not appear.
I repeat: qrmin and qrmax are set by the person at will, well, that's how I wrote the program. And from them should get

and

, but I accept that pmin=0, I have the right, just add to myself work, nothing more. But of course
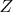
is not zeroed, it remains

.
So, rather, why are we not interested in eg

? Which is to say, why are we only interested in

?
Because I took the conditions

(which of

to choose is greater and which is less is arbitrary, I took

). With these conditions there is no way we can get

. And the condition

is due to the fact that we have already placed all the smaller primes in the pattern.
All possible variants

can be eliminated at once for all patterns by a single enumeration of

up to

, even if one does not believe my proofs from page 140 of this thread. Or one can of course relax the conditions on qrmin and qrmax here as well.
-- 22.11.2022, 00:37 --Program:
Код:
qrall=Set([2*5,2*7,2*11,3*5,3*7,3*11,5*7,5*11,7*11]); pmin=1e9; pmax=sqrt(stop/vecmin(qrall));\\qrall - sorted vector from min to max
{forprime(p=pmin,pmax,
foreach(qrall,qr,
h=p^2*qr; nn=round(h/32); if(h>stop, qrall=setminus(qrall,[qr]); break, !ispseudoprime(nn), next);\\To accelerate, delete a value that is too large and interrupt the loop.
h=nn*32; x=h%18;
if(x==2, if(!ispseudoprime((h-2)/18) || numdiv(h+2)!=12, next);
, x==16, if(!ispseudoprime((h+2)/18) || numdiv(h-2)!=12, next);
, next;
);
if(numdiv(h-1)!=12 || numdiv(h+1)!=12, next);
print("32x=",h);
);
if(#qrall==0, break);\\If qrall is empty then exiting
)}
Estimate work time is 4h.