Универсальное свойство дискретной топологии

[Mysterious Light]

Добрый день!

Задался вопросом, как выглядят универсальные непрерывные функции из топологического пространства $A$ в функтор $F: \mathrm{Set}\to\mathrm{Top}$, который наделяет множество дискретной топологией.
Иными словами, интересует $B$ с дискретной топологией и непрерывная функция $p: A\to B$ такие, что любая непрерывная функция $f: A\to X$ в произвольное $X$ с дискретной топологией однозначно раскладывается в композицию $f = g\circ p$, где $g: B\to X$.

Если $A$ имеет тривиальную топологию, то $B$ — точка. Действительно, непрерывность $g: A\to X$ означает, что $g(x)=\mathrm{const}$, а значит, $\mathrm{Hom}_{\mathrm{Top}}(A,X)\simeq X \simeq \mathrm{Hom}_{\mathrm{Set}}(1, X)$.

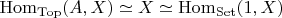
Если на пространстве $A$ есть база из непересекающихся непустых открытых множеств $\{ I_k\}_k$, то $B$ — это сама база, $p(x) = I_k \Leftrightarrow x\in I_k$ (определение корректно).
Каждая непрерывная $f: A\to X$ на каждом $I_k$ имеет постоянное значение $\{ y_k \} = f(I_k)$. Определим $g(I_k) = y_k$, тогда $f = g\circ p$, причём такая функция единственна.

Если $A$ — связное двоеточие, то $f: A \to X$ непрерывно только при $f = \mathrm{const}$. Поэтому $B = 1$.

Вопрос: правильно ли я рассуждаю и что делать в общем случае?

[Slav-27]

Правильно, попробуйте $A=\mathbb Q$.

[Mysterious Light]

Пробую.

Непрерывность в дискретное $X$ означает, что $\forall e\in X (f^{-1}(e) = \bigcup_k (a_k, b_k))$. У каждой точки $x$ есть окрестность, в которой $f = \mathrm{const}$
Предположение: множество $f^{-1}(e)$ не содержит граничных точек. Действительно, если $x\in\mathbb{Q}$ — граничная точка $f^{-1}(e)$, то или $f(x) = e$ и тогда $x$ внутренняя, или же $f(x) \neq e$ и тогда $x$ внешняя.

Поэтому $f_{-1}(e) = \varnothing$ или $\mathbb{Q}$.
Получается, что непрерывными могут быть тоже только константы и $B$ — точка.

Ещё попытка:
Если $A = \sum A_k$, то $\mathrm{Hom}(A,X) \simeq \prod_k \mathrm{Hom}(A_k,X)$. Пусть $p_k: A_k\to B_k$ универсальны, тогда $p = \langle p_1, p_2, \ldots \rangle$. Насколько я понимаю, это работает всегда, когда сумма определена:

$$\begin{aligned}\mathrm{Hom}(A_1 + A_2, FX) &\simeq \mathrm{Hom}(A_1, FX) \times \mathrm{Hom}(A_2, FX) \simeq \\ &\simeq \mathrm{Hom}(B_1, X) \times \mathrm{Hom}(B_2, X) \simeq \\ &\simeq \mathrm{Hom}(B_1 + B_2, X).\end{aligned}$$

Проверил, у Маклейна подобная теорема не сформулирована ни в тексте, ни в задачах.

Мне кажется, здесь всё опирается на возможность разбить топологическое пространство $A$ на семейство открытых множеств. Для односвязных пространств $B = 1$. Могу предположить, что $B$ перечисляет компоненты связности.

[Slav-27]

Mysterious Light в сообщении #1569147 писал(а):

Получается, что непрерывными могут быть тоже только константы

Нет.

[Mysterious Light]

Функция $f$ порождает отношение $a\sim b \Leftrightarrow f(a) = f(b)$, которая в свою очередь порождает фактор-множество $\mathbb{Q}/\sim$, состоящее из попарно непересекающихся множеств $\{ f^{-1}(e) | e \in \mathrm{Im}\, f \}$.
Если $f: \mathbb{Q}\to X$ непрерывна и $X$ имеет дискретную топологию, то по определению $f^{-1}(e)$ открыто в $\mathbb{Q}$, потому что $\{ e \}$ открыто в $X$. Значит, $\mathbb{Q}/\sim$ — это открытое покрытие из попарно непересекающихся множеств.
Существуют нетривиальные покрытия, например, $\{ (-\infty, \sqrt{2}), (\sqrt{2}, \infty) \}$. У таких покрытий нет граничных точек, что является особенностью $\mathbb{Q}$ как неполного пространства.
Справедливо и обратное: любое непересекающееся открытое покрытие порождает непрерывную функцию $f: \mathbb{Q}\to X$.

Несмотря на то, что у меня нет ответа на первоначальный вопрос, тему можно закрывать.

[Slav-27]

Да, поэтому для $A=\mathbb Q$ такого $B$ нет.

Mysterious Light в сообщении #1569407 писал(а):

собенностью $\mathbb{Q}$ как неполного пространства.

Не неполного, а несвязного: пространства, на которых только постоянные непрерывные функции, -- это в точности связные пространства. $\mathbb Q$, наоборот, вполне несвязно: его компоненты связности -- это точки.

По поводу первоначального вопроса: если пространство связных компонент $A$ дискретно (иными словами, $A$ локально связно), то оно и будет $B$ (и для локально связных пространств получается цепочка из 3 сопряжений: $\pi_0$ (множество связных компонент) -- снабжение множества дискретной топологией -- подлежащее множество топологического пространства -- снабжение антидискретной топологией). А для не локально связных -- увы.

[Mysterious Light]

Спасибо