Не первый день уже не могу вкурить пункт 3.7. у Маклейна. Неравномерно сложные параграфы попадались и раньше, но этот совсем какой-то зубодробительный. Приведу цитату прямо с начала.
Маклейн, стр.92 писал(а):
3.7. Копределы представимых функторовПолезность представимых функторов
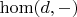
хорошо видна из следующего основного результата о функторах со значениями в категории множеств.
Теорема 1.
Любой функтор  из малой категории
из малой категории  в категорию множеств можно представить (каноническим образом) как копредел диаграммы представимых функторов
в категорию множеств можно представить (каноническим образом) как копредел диаграммы представимых функторов 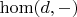 для объектов
для объектов  из
из  .
.Доказательство: Вначале построим для данного

искомую категорию диаграмм (для копредела)

в виде так называемой категории элементов из

. А именно, это категория запятой

(см. диаграмму (3) в § 2.6), в которой объектами служат пары

, где

, а стрелками

- те стрелки

из

, для которых

(более кратко,

). Мы утверждаем теперь, что данный функтор

является копределом диаграммы в категории

, которая соответствует функтору

Каждый объект

переходит в

-функтор

, а каждая стрелка

- в индуцированное естественное преобразование

. В силу изоморфизма Йонеды

существует конус в категории

с основанием

и вершиной

, который на нижеприведенной диаграмме изображен стрелками, идущими в

(внизу слева):
![$$\xymatrix{J: \ar[d]_{M}& (d, x) \ar[d]_{} & (d', x') \ar[d]^{} \ar[l]_{f^{*}} \\\mathbf{Set}^D: & D(d, -) \ar[d]_{y^{-1}x} \ar[dr]_{y^{-1}x'} & D(d', -) \ar[l]_{f^{*}} \ar[d]^{y^{-1}z'} \ar[dl]_{y^{-1}z} \\ . & K & L \ar[l]^{\theta}}$$ $$\xymatrix{J: \ar[d]_{M}& (d, x) \ar[d]_{} & (d', x') \ar[d]^{} \ar[l]_{f^{*}} \\\mathbf{Set}^D: & D(d, -) \ar[d]_{y^{-1}x} \ar[dr]_{y^{-1}x'} & D(d', -) \ar[l]_{f^{*}} \ar[d]^{y^{-1}z'} \ar[dl]_{y^{-1}z} \\ . & K & L \ar[l]^{\theta}}$$](https://dxdy-01.korotkov.co.uk/f/0/4/f/04fb4f197a95e14906c88526efdb935282.png)

Мы утверждаем, что этот конус определяет копредел для

.
Мне тут непонятно большое число вещей, поэтому буду разбираться последовательно.
1. Зачем писать словосочетание "представимый функтор
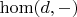
"?
Цитата:
Полезность представимых функторов
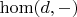
хорошо видна
Цитата:
как копредел диаграммы представимых функторов
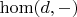
для объектов
Представимый функтор - это функтор, в который существует естественный изоморфизм из ковариантного

-функтора. Возьмем, собственно, сам ковариантный

-функтор
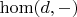
. Очевидно же, что он представимый, т.к. в него существует естественный изоморфизм из него же самого - просто тождественный изоморфизм (или по-другому единичная стрелка, если рассматривать этот

-функтор как объект категории функторов). Правильно ли я проинтерпретировал это словосочетание "представимый функтор
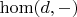
"? А то вдруг тут имеется в виду что-то другое.
2.
Цитата:
Вначале построим для данного

искомую категорию диаграмм (для копредела)

в виде так называемой категории элементов из

. А именно, это категория запятой

Как строится категория запятой

мне понятно. Верно ли, что в этом фрагменте текста утверждается, что

?