Одна из наиболее часто встречающихся проблем спектрального Фурье-анализа связана с растеканием спектра, когда сигнал не попадает на "гребёнку" базисных функций. Происходит это из-за того, что дискретный Фурье действует на самом деле не на отрезке, а на кольце, получающимся замыканием концов этого отрезка. Когда компонента сигнала не совпадает по частоте с базисной функцией (другими словами, когда длина отрезка разложения не кратна периоду этой компоненты) на стыке концов отрезка у сигнала возникают изломы и разрывы. Как известно, это очень "шумные" особенности в сигнале: разрыв затухает пропорционально

, а излом (разрыв первой производной) —

. Наглядный пример (зелёный сигнал второго графика — это синий сигнал первого графика, сдвинутый циклически на пол отрезка разложения; на третьем графике — спектры обоих сигналов, наложенные друг на друга):
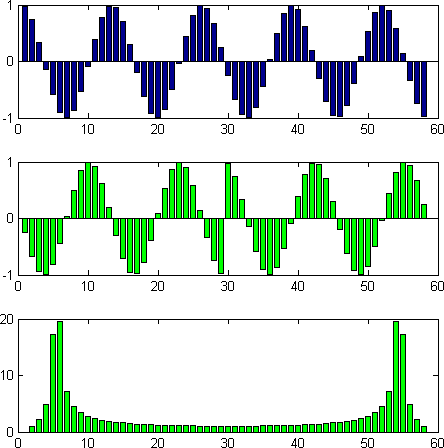
Код в Матлабе, если кто-то захочет поиграться с картинкой:
clc
clearvars
format compact
num = 58;
xx = ((1 : num)' - 0.5) / num;
yy1 = cos (2 * pi * xx * 4.5);
yy2 = [yy1(num / 2 + 1 : end); yy1(1 : num / 2)];
subplot (311)
bar (yy1)
subplot (312)
bar (yy2, 'g')
subplot (313)
bar (abs (fft (yy1)))
hold on
bar (abs (fft (yy2)), 'g')
hold off
Решением этой проблемы являются
всевозможные оконные функции. Умножение на оконную функцию приводит к тому, что сигнал на стыкуемых концах отрезка зануляется, что устраняет разрывы и изломы. Пики спектров немного уширяются (на две спектральные линии), за то сами пики затухают с удалением от своего центра гораздо быстрее.
Это хорошо проверенное и надёжное решение, которым все пользуются. Однако, у него есть один большой недостаток: потеря информации при занулении участков сигнала. Порой, когда имеющаяся информация и так не велика, такая потеря может быть недопустима. В связи с этим, я подумал: а какая есть альтернатива оконным функциям для борьбы с растеканием спектра? Нельзя ли вместо зануления сигнала, наоборот, дополнить его выдуманным сигналом, чтобы на стыках была непрерывность и гладкость?
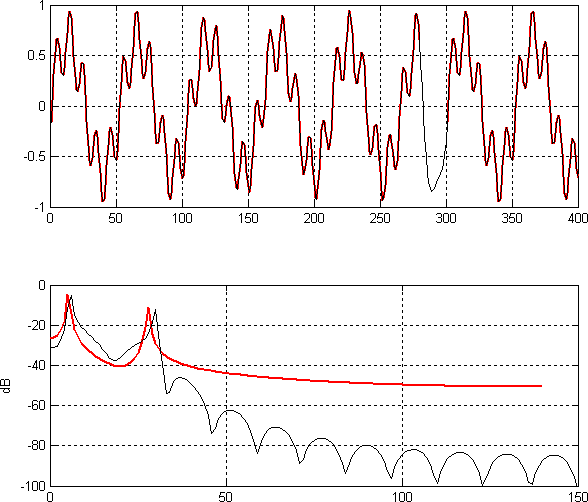
На вскидку пришла идея заполнить дополнительную область кольца полиномом, проходящим через стыкуемые концы сигнала. Не очень изящное, но легко реализуемое для эксперимента решение:
clc
clearvars
format compact
num = 280;
num_ex = 20;
cyc1 = 5.25;
amp1 = 0.65;
cyc2 = 27.75;
amp2 = -0.3;
nn = (1 : num)';
sgnl =...
amp1 * sin (2 * pi * cyc1 * nn / num) +...
amp2 * cos (2 * pi * cyc2 * nn / num);
spct = fft (sgnl);
spct_a = 2 * abs (spct (1 : num / 2 + 1)) / num;
sgnl_ex = [sgnl; zeros(num_ex, 1)];
pnn = [(-4 : 0)' + num, (1 : 5)' + num + num_ex];
pyy = [sgnl((-4 : 0) + num), sgnl(1 : 5)];
pol = polyfit (pnn, pyy, 7);
%sgnl_ex (num + (1 : num_ex)) = sgnl_ex (num) + (sgnl_ex (1) - sgnl_ex (num)) * (1 : num_ex) / num_ex;
sgnl_ex (num + (1 : num_ex)) = polyval (pol, num + (1 : num_ex)');
spct_ex = fft (sgnl_ex);
spct_ex_a = 2 * abs (spct_ex (1 : (num + num_ex) / 2 + 1)) / (num + num_ex);
subplot (2, 1, 1)
plot (sgnl, 'r', 'LineWidth', 2)
hold on
plot ((1 : 100) + num + num_ex, sgnl(1 : 100), 'r', 'LineWidth', 2)
plot ([sgnl_ex; sgnl_ex(1 : 100)], 'k')
hold off
grid on
subplot (2, 1, 2)
plot (0 : num / 2, 20 * log10 (spct_a), 'r', 'LineWidth', 2)
hold on
plot (0 : (num + num_ex) / 2, 20 * log10 (spct_ex_a), 'k')
hold off
ylim ([-100, 0])
grid on
ylabel ('dB')
Результаты довольно воодушевляющие. Видно, что у дополненного сигнала в дали от пиков спектр затухает гораздо быстрее, чем у исходного. Можно полагать, что перекрытие спектров двух компонент стало не таким сильным и их разделение упростилось.
Стоит сделать несколько важных наблюдений. Поскольку к сигналу добавляется промежуток с ненулевыми значениями, то суммарная мощность спектра растёт. При этом большая часть спектра теряет мощность. Очевидно, что старая "расплывшаяся" мощность, а так же новая добавленная идут в область с пиками компонент сигнала. Другими словами, спектр стекается обратно в пики. Так же важно отметить, что никакой новой информации в процессе дополнения не возникает. То, как именно дополняется новая область с сигналом, определяется именно самим сигналом, в первую очередь тем, где находятся его пики, то есть, куда мы хотим, чтобы собирался спектр, а где мы хотим, чтобы он занулялся. Это, в некотором смысле, волевое решение, принимаемое на основе имеющегося спектра, таким образом, дополнение сигнала — операция нелинейная. В отличие от оконных функций.
Конечно, используемые мной выше полиномы — это очень неудобные и ненадёжные функции. По многим причинам. Хотелось бы что-то более универсальное, связанное собственно со спектром сигнала. Какие в этом плане могут быть варианты? Что вообще, про такой подход можно сказать? Может, я изобретаю велосипед и всё давно продумано и доказано?