Добрый день.
Я сейчас пытаюсь исследовать равномерную сходимость ряда

на промежутке

.
Как мне кажется, этот ряд на указанном промежутке равномерно сходится.
Чтобы это подтвердить, я хочу доказать равномерную сходимость рядов

и

, а потом сказать, что изначальный ряд сходится равномерно, так как является их суммой.
Но я смог доказать равномерную сходимость этих рядов только на промежутке

, а на интервале

у меня возникают проблемы.
Первый мой вопрос связан с тем, могу ли я отдельно доказать сходимость на
![$(0; 1]$ $(0; 1]$](https://dxdy-01.korotkov.co.uk/f/0/6/3/06373f66178eb84c67f19d1e4ca13bdf82.png)
и на

, а потом сделать вывод, что ряд сходится равномерно на

?
Я предположил, что да, и решил доказывать с помощью признака сравнения:

, для второго ряда аналогично.
Ну и теперь мой второй вопрос: могу ли я сказать, что

- это степенной ряд, проведя замену

?
Если да, то мы знаем, что этот ряд равномерно сходится при

, то есть при
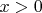
, а значит равномерно сходится на
![$(0; 1]$ $(0; 1]$](https://dxdy-01.korotkov.co.uk/f/0/6/3/06373f66178eb84c67f19d1e4ca13bdf82.png)
и исходный ряд. Со вторым рядом разбираемся аналогично.
Если какое-то из моих предположений неверно, то, пожалуйста, подскажите в какую сторону смотреть. Может быть, я вообще пытаюсь доказать ложное утверждение?