Простой "вывод" правила Бора-Зоммерфельда

[madschumacher]

Добрый вечер.

Как обычно, прошу прощения за беспокойство и задачу тупых вопросов, особенно в неподходящее время. Я тут давеча пытался (в квазипедагогических) целях найти какой-нибудь простой вывод условий квантования Бора-Зоммерфельда, в частности некую простую модель для масловской поправки, но к сожалению, даже в "Как понимать квантовую механику", всё не настолько просто. В результате у меня появился альтернативный (в плохом смысле слова) вывод сего правила. Поэтому я хотел бы узнать мнение, насколько он идиотичен, и можно ли его использовать для "квазивывода" правил Бора-Зоммерфельда на реальных людях.

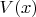
Итак, в качестве стартовой точки, введём операторы сдвига по координате для частицы с энергией $E$ в одномерном потенциале $V(x)$. Для движения частицы из координаты $x$ слева направо до координаты $x'$, этот оператор определим как

$$\hat{U}_{x \rightarrow x'} = \exp\left( -\frac{i}{\hbar} \int \limits_{x}^{x'} |p| dx \right)$$

,
где $|p(x)| = |\sqrt{2m (E - V(x)) }|$ -- это абсолютное значение импульса в точке $x$. Очевидно, что это просто нулевое приближение ВКБ. Аналогично, для частицы движущейся из $x'$ в $x$ справа налево, у нас будет оператор

$$\hat{U}_{x \leftarrow x'} = \exp\left( +\frac{i}{\hbar} \int \limits_{x'}^{x} |p| dx \right) = \exp\left( -\frac{i}{\hbar} \int \limits_{x}^{x'} |p| dx \right) = \hat{U}_{x \rightarrow x'} $$

,
т.е. этот оператор у нас ни в одном глазу не унитарный.

Но давайте тогда проследуем за волновой функцией, будто бы за движением частицы. Допустим, у нас имеется потенциальная яма, где точками поворота частицы с энергией $E$ ($V(x) = E$) у нас являются $x_{\min}$ слева и $x_{\max}$ справа (см. рис. ниже). Значит, $x_{\min} \leq x \leq x_{\max}$ -- это классически разрешённая область, а $x \notin [x_{\min},x_{\max}]$ -- это классически запрещённая область.


Теперь, давайте попробуем "проследить" за эволюцией волновой функции нашей частицы при движении по оси $x$, скажем от точки $x=x_{\min}$ (см. рис. ниже).

1. Допустим, "начальным условием" у нас является, что "волновая функция" для нашей частицы, начинающей полёт направо это $\psi_{0}^{\rightarrow}$.
   
2. Если мы долетим до точки $x_{\max} = L + x_{\min}$, то получим волновую функцию $\psi_{L}^{\rightarrow} = \hat{U}_{x_{\min} \rightarrow x_{\max}} \psi_{0}^{\rightarrow} = \exp\left(-\frac{i}{\hbar} \int \limits_{x_{\min}}^{x_{\max}} |p| dx \right)\psi_{0}^{\rightarrow}$. Очевидно, как и ожидалось, у нас просто добавляется фаза, равная половине $I = \oint p dx = 2 \int \limits_{x_{\min}}^{x_{\max}} |p| dx$, т.е. мы можем переписать получившийся результат как $\psi_{L}^{\rightarrow} = \exp\left(-\frac{i}{2\hbar} I \right)\psi_{0}^{\rightarrow}$.
   
3. Далее у нас частица разворачивается, но поскольку у нас она может заходить в классически запрещённую область, мы получим
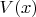   для развернувшейся частицы в точке $x_{\max}$ волновую функцию $\psi_{L}^{\leftarrow} = C_{\hookleftarrow} \psi_{L}^{\rightarrow}$. Будем считать, что потенциал $V(x)$ неубывает с двух сторон, поэтому никаких новых ям/бесконечных долин, куда может мигрировать наша частица, у нас нет, поэтому всё, что долетело до точки поворота, в итоге полетит обратно. Это означает, что $|C_{\hookleftarrow}|^2=1$, и значит мы можем переписать $C_{\hookleftarrow} = \exp(i \varphi_{\hookleftarrow})$, т.е. $\psi_{L}^{\leftarrow} = \exp(i \varphi_{\hookleftarrow}) \psi_{L}^{\rightarrow}$ (в точках поворота у нас набегает некая дополнительная фаза).
   
4. Потом мы долетаем обратно налево до $x_{\min}$, получая $\psi_{0}^{\leftarrow} = \hat{U}_{x_{\min} \leftarrow x_{\max}} \psi_{L}^{\rightarrow} = \exp\left(-\frac{i}{2\hbar} I \right) \psi_{L}^{\rightarrow}$.
   
5. И под конец, наша частица разворачивается уже на левой точке поворота, приобретая дополнительную фазу $C_{\hookrightarrow} = \exp(i \varphi_{\hookrightarrow})$, в результате чего мы получаем
   $\psi_{0}^{\rightarrow} = \exp(i \varphi_{\hookrightarrow}) \psi_{0}^{\leftarrow} $.
   

Собирая воедино начало и конец нашего полёта, мы получаем уравнение:

$$\psi_{0}^{\rightarrow} = \exp\left(i \varphi_{\hookrightarrow} -\frac{i}{2\hbar} I + i \varphi_{\hookleftarrow} -\frac{i}{2\hbar} I \right) \psi_{0}^{\rightarrow} $$

Отсюда, мы получаем наше условие квантования:

$$\frac{I}{\hbar} = \frac{1}{\hbar} \oint p dx = 2 \pi \cdot n + \varphi_{\hookrightarrow} + \varphi_{\hookleftarrow}$$

где $n \geq 0$, поскольку $I \geq 0$.

Но при этом мы всё ещё не нашли эти фазы, которые частица преобретает на поворотах. Для этого мы возьмём грязный-прегрязный трюк. Рассмотрим частицу на правой точке поворота $x_{\max}$. Скажем, что она проходит до некой точки $x'> x_{\max}$, разворачивается, и идёт обратно. При таком походе с начальной волновой функцией $\psi_{L}^{\rightarrow}$ она преобретает дополнительную фазу из уравнения
$\psi_{L}^{\rightarrow}(x') = \hat{U}_{x_{\max} \leftarrow x'} \hat{U}_{x_{\max} \rightarrow x'} \psi_{L}^{\rightarrow} = \exp \left( - \frac{2i}{\hbar} \int \limits_{x_{\max}}^{x'} |p| dx \right) \psi_{L}^{\rightarrow}$
И чтобы найти все эти фазы, нам нужно просуммировать все волновые функции $\psi_{L}^{\rightarrow}(x')$, получающиеся при походах до каждой точки в классически-запрещённой зоне, т.е.
$\psi_{L}^{\rightarrow} = \exp(i\varphi_{\hookleftarrow}) \psi_{L}^{\leftarrow} = \int \limits_{x_{\max}}^{\infty} \psi_{L}^{\rightarrow}(x') dx' $
Естественно, этот интеграл посчитать нормально невозможно. Поэтому мы применим ещё один грязный трюк. Обозначим $2\int \limits_{x_{\max}}^{x'} |p| dx =S(x')$. Поскольку мы считаем потенциал неубывающим, то в классически-запрещённой области, эта функция тоже будет неубывающей. При этом, мы можем выразить примерное поведение настоящей волновой функции в этой области, оно даётся выражением
$\psi(x') = T(x') \psi_{L}^{\rightarrow}$, где $T(x') = \exp\left(-\frac{2}{\hbar}\int_{x_{\max}}^{x'} |p|dx\right) = \exp\left(-\frac{S }{\hbar}\right)$ -- это коэффициент прохождения через стенку. Поэтому давайте вместо искомого интеграла будем брать

$$ \psi_{L}^{\rightarrow} = \int \limits_{x_{\max}}^{\infty} \psi_{L}^{\rightarrow}(x') dx' \approx \frac{ \int \limits_{x_{\max}}^{\infty} T(x')^{\gamma} \psi_{L}^{\rightarrow}(x') dx' }{\int \limits_{x_{\max}}^{\infty} T(x') dx' } \ , $$

где знаменатель у нас появляется для нормировки, а $0 \leq \gamma $ -- это параметр регуляризации (?), который мы потом устремим к нулю. Сверху и снизу, заменим интегрирование по координате на интегрирование по $S$, и будем надеяться, что эффекты от соответствующей замены координат у нас сократятся сверху и снизу в дроби. Т.е.

$$ \psi_{L}^{\rightarrow} \approx \frac{ \int \limits_{0}^{\infty} \exp\left( -\frac{1}{\hbar} ( \gamma + i) S \right) dS}{\int \limits_{0}^{\infty} \exp\left( -\frac{S}{\hbar} \right) dS } \cdot \psi_{L}^{\rightarrow} = \frac{\gamma - i }{\gamma^2 + 1} \psi_{L}^{\rightarrow} \ . $$

Кладя $\gamma = 0$, мы получаем $\psi_{L}^{\rightarrow} = -i \psi_{L}^{\rightarrow} = \exp(-i \pi/2) \psi_{L}^{\rightarrow} $. То же самое получится и с другой точкой поворота, поэтому на выходе мы получим искомое условие квантования Бора-Зоммерфельда:

$$\frac{I}{\hbar} = \frac{1}{\hbar} \oint p dx = 2 \pi \cdot n + \pi$$

Если же у нас бесконечный ящик, то никакого набегания фаз от частиц в запрещённой области не происходит, и $C_{\hookleftarrow} = C_{\hookrightarrow} = 1$, откуда у нас вылезают как обычно условия квантования

$$\frac{I}{\hbar} = \frac{1}{\hbar} \oint p dx = 2 \pi \cdot n $$

Если кто-то видел где-то такое, или это выглядит хоть как-то нормально, или если это очевидный бред, пожалуйста, сообщие об этом. Спасибо за внимание.