Но что странно: функция резко растет на отрезке

от 5.84 до 5.85, как будто она там вообще разрывная, может быть, какой-то вычислительный глюк.
При этих значениях угла максимум функции

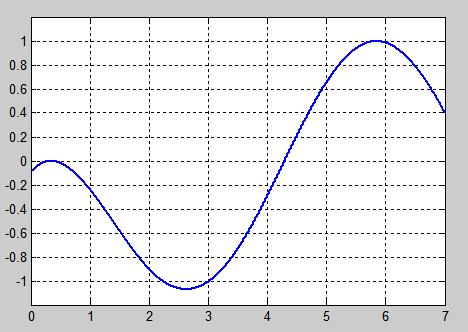
подходит снизу к нулю и пересекает его. При этом вблизи нуля рождается пара корней, которая даёт наибольший вклад в сумму ниже (за счёт своей близости к нулю).

Поскольку ноль пересекается гладкой функцией с квадратичной выпуклостью вверх, то рост суммы вблизи этого значения угла происходит почти (с поправкой на экспоненту) как рост квадратного корня вблизи (его) нуля. Пока мне не совсем понятно, есть ли там излом или нет. Кажется, что есть, но надо проверять.
 -- 25.06.2022, 19:29 --
-- 25.06.2022, 19:29 --ноль пересекается гладкой функцией с квадратичной выпуклостью вверх
И это, кстати, очень и очень плохо для численного расчёта этих корней, поскольку обращаемая функция является разностью больших чисел, которая близка к нулю. Тут надо что-то хитрое сгородить (например, вывернуть функцию наизнанку как-нибудь), хотя бы до тех пор, пока нули не разойдутся на приличное расстояние, иначе точности никакой не будет.
Излом в точке рождения корней, разумеется есть, причём справа в точке производная искомой функции угла обращается в бесконечность, а сама функция справа в эпсилон-окрестности ведёт себя как квадратный корень (с коэффициентом).