Задача про момент сил

[Aael]

Что не так? Не сходится ответ с задачей из учебника "Биология Физика Химия. Сборник задач и упражнений 7-9." 2-е издание 2021 Иванеско:

Цитата:

Два грузчика несут рулон линолеума длиной $L = 5\ \text{м}$ ($l=L/2$) и массой $m=64\ \text{кг}$. Один грузчик держит рулон на расстоянии $a=80\ \text{см}$ от его конца, другой - на расстоянии $b=1\ \text{м}$ от противоположного конца. Найдите силу давления рулона, испытываемого каждым грузчиком.
Ответ:
$\displaystyle F_2 = \frac{mgL}{2(L-b)}=\frac{64\cdot9,\!8\cdot5}{2(5-1)}=392\ \text{Н}$
$\displaystyle F_1 = mg - F_2 = 64\cdot 9,\!8 - 392=235,\!2\ \text{Н}$

Рулон без грузчиков "падает" в поле гравитации "вниз" без вращения. Чтобы описать такое движение можно рассматривать его как невесомый отрезок с приложенной силой тяжести к центру (масс). Эту силу можно переносить, раскладывать на конечное число других сил, приложенных к каким-то точкам отрезка, итд - это все эквивалентные модели, можно брать любую из них:

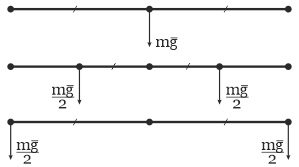
Подключаются силы от грузчиков, система приходит в состояние покоя, и можно выписывать уравнения моментов сил в любой точке отрезка - нигде ничего не вращается, и сумма моментов равна нулю. Для простоты - в точках приложения сил:

$\displaystyle\left\{ \begin{array}{l} (l-a+l-b)F_1+0\cdot F_2-(l-a)mg=0 \\ (l-a+l-b)F_2+0\cdot F_1-(l-b)mg=0 \\ \end{array}\right.\Rightarrow \left\{ \begin{array}{l} F_1=\frac{l-a}{2l-(a+b)}mg=\frac{L-2a}{L-(a+b)}\frac{mg}2=333,\!2\ \text{Н} \\ F_2=\frac{l-b}{2l-(a+b)}mg=\frac{L-2b}{L-(a+b)}\frac{mg}2=294,\!0\ \text{Н} \\ \end{array}\right. $
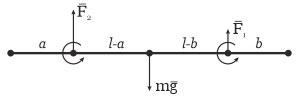
Или, например, можно перенести силы от грузчиков в центр, добавив пары, сохраняющие вращение. Тогда получим дополнительное уравнение равенства нулю равнодействующей силы (и нулевой момент относительно центра масс):

$\displaystyle\left\{ \begin{array}{l} F_1+F_2-mg=0 \\ (l-a)F_2-(l-b)F_1=0 \\ \end{array}\right.\Rightarrow \left\{ \begin{array}{l} F_1=\frac{l-a}{l-b}F_2 \\ F_2 + \frac{l-a}{l-b}F_2=mg \end{array}\right.\Rightarrow \left\{ \begin{array}{l} F_1=\frac{l-a}{2l-(a+b)}mg=\frac{L-2a}{L-(a+b)}\frac{mg}2 \\ F_2=\frac{l-b}{2l-(a+b)}mg=\frac{L-2b}{L-(a+b)}\frac{mg}2 \end{array}\right. $
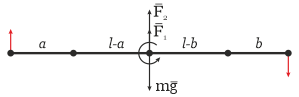
Собственно, можно как угодно делать. Дальше говорим, что по третьему закону Ньютона силы давлений на грузчиков равны численно $F_1$ и $F_2$. Или нет? Заранее спасибо!

[sergey zhukov]

Aael
Как минимум странно, что в ответ из учебника не вошло $a$. Так быть не может. По моему, ответ в учебнике записан почему-то для $a=0$

[Aael]

sergey zhukov в сообщении #1556861 писал(а):

Как минимум странно, что в ответ из учебника не вошло $a$. Так быть не может. По моему, ответ в учебнике записан почему-то для $a=0$

ну, да.. похоже на то. Я решил они могли её где-то подставить в формулу. Плюс это второе издание, и вероятность опечаток меньше. Может они как-то по-другому тот рулон несли (иллюстраций в учебнике нет к задаче, если что).

[svv]

Грузчики названы "один" и "другой", поэтому логичнее обозначить силы соответственно $F_1$ и $F_2$, а не наоборот.

[Arks]

Aael
Я не очень понял с этими перенесениями сил, но по расчетам все норм. Общее правило таково, что виртуальная работа по всевозможным бесконечно малым перемещениям стержня (при котором его концы двигаются только по вертикали) равна нулю. Число степеней свободы равно двум, и это может быть как сумма вертикальных смещений стержня и поворота отн. какой-то точки, либо же сумма двух поворотов. Вы собственно эти два варианта и показали.

Aael в сообщении #1556858 писал(а):

Дальше говорим, что по третьему закону Ньютона силы давлений на грузчиков равны численно $F_1$ и $F_2$. Или нет?

Нет, это силы давления на рулоны со стороны грузчиков равны по третьему закону, а мы уже все нашли)