EminentVictoriansЕсли Вы используете именно неопределённые интегралы (точнее первообразные), то переход

— это, фактически, и есть правило Лопиталя, которое Вы стремитесь доказать. То есть да, правило Лопиталя — это формализация (невнятного) правила «если

, то

».
Можно обойтись только первообразными, но тогда вообще нет нужды упоминать интегралы (если первообразная

известна, то зачем использовать для неё громоздкое обозначение

?). Исходное утверждение (и другие правила Лопиталя) можно вывести из такого: Пусть

при
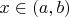
, причём существуют конечные правые пределы

. Тогда

при
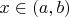
. Тут достаточно теоремы Лагранжа вместо теоремы Коши.
Другими словами, правило Лопиталя можно вывести из правила интегрирования неравенств, которое есть как для определённого интеграла (

), так и для неопределённого (

).