Вопрос не очень понятен. Например, пусть есть множество A=

, упорядоченное так, что

. И определим функцию

, положив
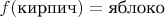
и

. Эта функция Вас устраивает?
Кстати, зависеть от параметра она никак не может, поскольку Вы хотите, чтобы она была задана именно на множестве

.