робастная оценка ков. матрицы

[AndreyL]

Дамы и Господа!

В робастной оценке ковариационной матрицы методом минимального определителя ковариаций (FAST-MCD и аналогичные), рекомендуемом ГОСТ-ом Р ИСО 16269-4-2017-4, предлагается объявлять выбросами те наблюдения, которые не попадают в 95.5%-ный доверительный эллипсоид. Эта же цифра 95.5% есть в работе [Rousseeuw, Peter & Driessen, Katrien. (1999). A Fast Algorithm for the Minimum Covariance Determinant Estimator. Technometrics. 41. 212-223. 10.1080/00401706.1999.10485670], а также в последующих работах по робастным оценкам ков. матриц. В функциях МАТЛАБ-а реализовано четыре алгоритма оценки, ни в одном из них не предусмотрена опция изменения этой вероятности. Как показали тесты на МАТЛАБ-е, все методы объявляют выбросами 2.5% валидных анализов. Вопрос - почему именно 95.5%, есть ли хоть какое-то объяснение? И почему величина доверительного эллипсоида не зависит от объема выборки?

[Евгений Машеров]

Почему 95.5% - объяснить просто, это (чуть округлённая) вероятность попадания в интервал $\pm 2\sigma$ (точное значение 95.4499736%). Почему именно 2, а не 3 или даже 5 сигм? Боюсь, условное соглашение, и постоянство его применения опирается на военную мудрость: "пусть и безобразно, зато однообразно!". Почему не зависит от объёма выборки - подозреваю, по той же причине. Чтобы у всех был одинаковый ответ, без возможности "подогнать под желаемое".

[AndreyL]

Прошу прощения, не 95.5, а 97.5%, т.е. остается 2.5%. Нашел, что раньше эта цифра появилась в работе [Peter J. Rousseeuw and Bert C. van Zomeren. Unmasking Multivariate Outliers and Leverage Points. Journal of the American Statistical Association, Vol. 85, No. 411 (Sep., 1990), pp. 633-639. https://doi.org/10.2307/2289995], опять же без пояснений.
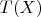
Интересно, что в этих работах утверждается, что квадрат расстояния Махаланобиса $D^2=(x-T(X))S(X)^{-1}(x-T(X))$ подчиняется распределению хи-квадрат, где $T(X)$ и $S(X)$ - оценки вектора средних и ковариационной матрицы по выборке. Но ведь это не верно, распределению хи-квадрат подчиняется $D^2=(x-A)\Sigma^{-1}(x-A)$, где $A$ и $\Sigma$ - истинные значения вектора средних и ковариационной матрицы. А если берутся оценки параметров, то распределения квадрата расстояния Махаланобиса совершенно другое. Или я не прав?

-- Пт апр 29, 2022 1:03 pm --

Евгений Машеров в сообщении #1553622 писал(а):

Почему не зависит от объёма выборки - подозреваю, по той же причине. Чтобы у всех был одинаковый ответ, без возможности "подогнать под желаемое".

Но вероятность вылететь за 97.5%-ный эллипсоид при одном испытании 2.5%, а при ста испытаниях 92%. В результате, фиксируя эллипсоид на уровне 97.5% на больших выборках получается не нормальное распределение, а усеченное нормальное, а у него другая ковариационная матрица.

[Евгений Машеров]

Тогда тоже понятно. 5% значимость отклонения.

[AndreyL]

Евгений Машеров в сообщении #1553631 писал(а):

Тогда тоже понятно. 5% значимость отклонения.

Почему 5%? Критерий хи-квадрат при обнаружении выбросов, т.е. в данном случае, односторонний.

-- Пт апр 29, 2022 1:31 pm --

Ведь квантиль распределения хи-квадрат с одной степенью свободы для вероятности 97.5% равен квадрату квантиля нормализованного нормального распределения для вероятности 98.75% (и для вероятности 1.25%), и равен 5.02389.

[Евгений Машеров]

Конкретное значение, боюсь, назначено чисто волевым решением, поскольку информация для более обоснованного вывода может быть недоступна, а одинаковость процедуры исключает возможность "подгонки под ответ".
Что до одинакового критерия при разных объёмах выборки - полагаю, представляется "засоренная выборка", в которой есть некоторый процент выбросов, и с ростом объёма выборки будет расти и число попавших в неё "засорений". Если их нет вообще - будут потери в выборке, но много их окажется, если выборка достаточно велика, и "отряд не заметил потери бойца".

[AndreyL]

Мои тесты показали, что в случае незасоренной выборки теряем 2.5% валидных значений, что, на мой взгляд, совсем не верно. Забавно, что тот-же ГОСТ для одномерных выборок предлагает критерий GESD, в приложении даже алгоритм приведен, и в этом критерии в явном виде учитывается объем выборки, правда, по-моему, не совсем корректно, но хоть какая-то попытка. Там весь смысл в последовательном использовании критерия типа Граббса, и на серии численных тестов [Bernard Rosner. Percentage Points for a Generalized ESD Many-Outlier Procedure. Technometrics Vol. 25, No. 2 (May, 1983), pp. 165-172. https://doi.org/10.2307/1268549] демонстрируется, что критическое значение для двух выбросов в выборке объема, например, 26, равно критическому значению для одного выброса в выборке объема 25 и трех значений в выборке объема 27. Это мне воспроизвести не удалось, но для одного выброса критические значения воспроизводятся. Почему не сделать аналогичный критерий для многомерной выборки? Там не на много сложнее.