Возможно также решение, не использующее пфаффиан. Выпишем определитель порядка

через перестановки. Возьмём одно слагаемое, в нём

множителей-элементов и ещё

. Множители могут быть "парные" (когда вместе с элементом
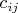
в произведение входит также

) и "непарные". Если в произведении есть хоть один непарный множитель, математическое ожидание произведения равно нулю. Значит, надо рассмотреть только случай, когда в слагаемом

пар (различных). Тогда матожидание их произведения равно

. Но есть ещё знак. Он определяется чётностью перестановки

, это даёт

, и матожидание слагаемого со знаком

. Остаётся только умножить на число способов разбиения множества

на неупорядоченные пары. А это как раз двойной факториал.