Оценка погрешности коэффициентов параболической регрессии

[apt]

Есть набор экспериментальных точек. По МНК находятся коэффициенты параболы $y=ax^2+bx+c$, описывающей данную зависимость.
Во-первых, как будет точнее назвать то уравнение, которое мы нашли - регрессия или аппроксимация?
Во-вторых как оценить погрешность коэффициентов $a,b,c$?
Если для линейной зависимости эти формулы есть много где

$$S_y^2=\frac{\sum_{i=1}^n (y_i-ax_i-b)^2}{n-m-1}$$

$$S_a^2=S_y^2\frac{\sum_{i=1}^n x^2}{n^2 \sigma_x^2}$$

$$S_b^2=S_y^2\frac{1}{n\sigma_x^2}$$

То для параболы нигде не могу найти
Куда копать?

[Евгений Машеров]

Я бы воспользовался общим выражением для регрессии $y=Xa+\varepsilon$
$\sigma^2(a)=\sigma^2(X^TX)^{-1}$
Где $\sigma^2(a)$ -дисперсия оценок коэффициентов (вернее, дисперсия по диагонали матрицы, а внедиагональные - ковариации оценок), а $\sigma^2$ это оценка дисперсии возмущающего фактора.

[apt]

Евгений Машеров в сообщении #1550538 писал(а):

Я бы воспользовался общим выражением для регрессии $y=Xa+\varepsilon$

Я так понимаю, X - матрица базисных функций, a - вектор коэффициентов, y - вектор значений, а $\varepsilon$ - вектор остатков?

[Евгений Машеров]

Да. Поискал что-то из старых учебников, когда особо выделять полиномиальную регрессию имело смысл - но у них фокус на расчётах, причём вручную, а не на оценке погрешностей коэффициентов.

[zykov]

apt в сообщении #1550525 писал(а):

Во-вторых как оценить погрешность коэффициентов $a,b,c$?

Сделайте самостоятельно.
Оценка коэффициента - это случайная величина. Посчитайте (или приближенно оцените) дисперсию этой случайной величины.
Ещё не мешало бы на матожидание посмотреть. В пределе большой выборки оно должно сходится к точному значению. Но для конечной выборки вполне может оказатся сдвинутым (что тоже даёт вклад в погрешность).

(В учебнике должен быть вывод погрешности для линейной регрессии. Попробуте его адаптировать для квадратичной.)

[apt]

Евгений Машеров в сообщении #1550538 писал(а):

$\sigma^2$ это оценка дисперсии возмущающего фактора.

А у нас не получается так, что дисперии оценок коэффициентов зависят только от x?
Если, опять же, я правильно понял, что

$$\sigma^2=\frac{\sum_i^N (x-\bar{x})^2}{N}$$

Как-то это странно

zykov в сообщении #1550576 писал(а):

Оценка коэффициента - это случайная величина. Посчитайте (или приближенно оцените) дисперсию этой случайной величины.

У меня на выходе после МНК - одно значение для каждого коэффициента. Как?

zykov в сообщении #1550576 писал(а):

(В учебнике должен быть вывод погрешности для линейной регрессии. Попробуте его адаптировать для квадратичной.)

О каком учебнике речь?

[Евгений Машеров]

apt в сообщении #1550578 писал(а):

Если, опять же, я правильно понял, что

Неправильно. Это оценка дисперсии эпсилона.

[apt]

Евгений Машеров в сообщении #1550592 писал(а):

Неправильно. Это оценка дисперсии эпсилона.

Т.е.

$$\varepsilon_i=y_i-f(x_i)$$

$$\bar{\varepsilon}=\frac{1}{n-1}\sum_{i=1}^{n-1} \varepsilon_i$$

$$\sigma^2=\frac{1}{n-1}\sum_{i=1}^{n-1}(\bar{\varepsilon}-\varepsilon_i)^2$$

n - число узлов (экспериментальных точек)

[Arks]

Евгений Машеров в сообщении #1550538 писал(а):

а $\sigma^2$ это оценка дисперсии возмущающего фактора.

Которую надо задать отдельно Т.е. формулы выше бессмысленны?

-- 16.03.2022, 22:51 --

apt
Давайте-ка рассмотрим простую модель. Пусть у нас есть априорное равновероятностное распределение координаты одной точки А на прямой, мы проводим измерение это координаты прибором, который к истинному значению координаты прибавляет нормальную погрешность с дисперсией $\sigma^2$. Сделали два измерения, получили показания $x_1$ и $x_2$. Теперь очевидно, что применяя ММП, какова будет наиболее вероятная оценка для истинной координаты (совпадающая с МНК), но вот ее дисперсия зависит от неизвестного $\sigma^2$, а эту сигму взять неоткуда

[Евгений Машеров]

Arks в сообщении #1550601 писал(а):

Которую надо задать отдельно Т.е. формулы выше бессмысленны?

Которую оценивают по данным, используя остаток от регрессии.

-- 17 мар 2022, 06:39 --

Arks в сообщении #1550601 писал(а):

Давайте-ка рассмотрим простую модель. Пусть у нас есть априорное равновероятностное распределение координаты одной точки А на прямой, мы проводим измерение это координаты прибором, который к истинному значению координаты прибавляет нормальную погрешность с дисперсией $\sigma^2$. Сделали два измерения, получили показания $x_1$ и $x_2$. Теперь очевидно, что применяя ММП, какова будет наиболее вероятная оценка для истинной координаты (совпадающая с МНК), но вот ее дисперсия зависит от неизвестного $\sigma^2$, а эту сигму взять неоткуда

А какое отношение данная модель имеет к обсуждаемой задаче?

[Александрович]

apt в сообщении #1550525 писал(а):

Во-первых, как будет точнее назвать то уравнение, которое мы нашли - регрессия или аппроксимация?

Аппроксимация это приближение исходных значений к аппроксимирующей функции регрессии.

[Евгений Машеров]

apt в сообщении #1550595 писал(а):

Евгений Машеров в сообщении #1550592 писал(а):

Неправильно. Это оценка дисперсии эпсилона.

Т.е.

$$\varepsilon_i=y_i-f(x_i)$$

$$\bar{\varepsilon}=\frac{1}{n-1}\sum_{i=1}^{n-1} \varepsilon_i$$

$$\sigma^2=\frac{1}{n-1}\sum_{i=1}^{n-1}(\bar{\varepsilon}-\varepsilon_i)^2$$

n - число узлов (экспериментальных точек)

"Тепло"!
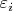
Только делить при расчёте сигмы надо не на $n-1$, а на $n-m$, где m - число параметров (проще всего это объяснить геометрически, случайность оценок данной модели проистекает из случайности эпсилонов, n штук $\varepsilon_i$ задают точку в n-мерном пространстве, а m параметров плоскость размерностью m, именно плоскость, несмотря на квадратичный и вообще любые нелинейные члены - поскольку модель линейна по коэффициентам, то есть отклонения от модели, невязки $e_i=y_i-\Sigma_j a_j x_{i,j}$ лежат в $n-m$-мерном пространстве, и если матожидание квадрата каждого равно $\sigma^2$, то для их, квадратов, суммы - $(n-m)\sigma^2$; соответственно, разделив сумму квадратов невязок на $n-m$, получим несмещённую оценку дисперсии).
Аналогично объясняется и вычитание единицы при расчёте дисперсии среднего, это учитывает, что по выборке из n элементов мы уже рассчитали один параметр - среднее.
А вот при расчёте среднего вычитать единицу не надо, надо делить на число наблюдений n.
Однако в данном случае это ни на что не влияет, поскольку рассматривается модель со свободным членом. Невязки соответствуют тому, что мы не смогли объяснить через регрессоры, и в силу использования МНК вектор невязок будет ортогонален всем векторам, образованным регрессорами. А так как свободный член - регрессор (даже если в вычислительной схеме обрабатывается особо), то вектор невязок ортогонален ему, так что сумма невязок заведомо равна нулю.

[Евгений Машеров]

Да, и ещё два замечания - в сообщении коллеги apt суммирование производится до $n-1$. Это неверно, там n величин. Может, конечно, он на C программирует, и цикл как раз до $n-1$, но тогда начинается с нуля.
И касательно формул для простой линейной модели - в первом сообщении в знаменателе $n-m-1$, я привожу формулу с $n-m$. Это не противоречие, просто часто для упрощения свободный член обрабатывают особо, вычитая средние из регрессоров и регрессанда, и обращая матрицу, построенную на центрированных регрессорах. Которых m, и один параметр - среднее (или, иначе говоря, материал для расчёта свободного члена, одного параметра). То есть в приведенной мной и коллегой формулах m отличается на единицу. Но, кстати, для простой линейной одномерной регрессии можно использовать m, но оно равно единице.

[apt]

Спасибо, помогло

[Евгений Машеров]

apt в сообщении #1550578 писал(а):

У меня на выходе после МНК - одно значение для каждого коэффициента. Как?

Случайность тут появляется постольку, поскольку в модели $y=Xa+\varepsilon$ случайными полагаются эпсилоны. То есть если мы многократно проводили бы измерения игреков при постоянной матрице иксов, каждый раз строя оценку, то наши оценки $\hat{a}$ были бы различными случайными величинами, характеризующимися матожиданиями и дисперсиями (дополнительное предположение, что распределение эпсилонов нормальное, делает нормальным и распределение оценок, как линейных функций от нормально распределённых величин, а это значит, что матожидание и дисперсия полностью их описывают). В действительности у нас единственное исследование, в котором мы можем оценить дисперсию эпсилонов (в предположении их нулевого матожидания и постоянства дисперсии; первое предположение "выбирается" свободным членом модели и существенно лишь для моделей без свободного члена, второе может на практике нарушаться и требовать использования взвешенного МНК). Но, зная оценку дисперсии, можем перейти к дисперсиям и ковариациям оценок, формула выше.

-- 18 мар 2022, 08:18 --

zykov в сообщении #1550576 писал(а):

Ещё не мешало бы на матожидание посмотреть. В пределе большой выборки оно должно сходится к точному значению. Но для конечной выборки вполне может оказатся сдвинутым (что тоже даёт вклад в погрешность).

Оценки МНК - несмещённые, матожидание равно истинному, независимо от размера выборки. Есть методы оценивания, отказывающиеся от требования несмещённости (например, ридж-регрессия - там смещённые оценки с меньшей дисперсией).