Уважаемые участники и гости форума, предлагаю Вашему вниманию вторую попытку доказательства великой теоремы Ферма.
1. Представление суммы  .
. Для любых натуральных

и

и любого нечетного простого

сумма

может быть представлена двумя способами

и

Рассмотрим сумму справа в (1). Если развернуть выражение, стоящее под знаком
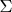
, то для значений показателя степени

выражение будет иметь относительно простой вид.
С ростом показателя степени выражения становятся все сложнее. Поскольку далее нам не потребуется точное выражение, определим его вид, из которого будет видно, что правая часть в (1) кратна лишь

.
При любом простом

число членов в сумме всегда четно и все симметрично расположенные члены имеют одинаковые коэффициенты. Скомбинировав все члены с одинаковыми коэффициентами, получим

Все биномиальные коэффициенты под знаком суммы кратны

. Действительно,

Поскольку

, то для всех

из этого диапазона

,
следовательно,

.
Все показатели степени

--- нечетные, следовательно, все

делятся на

. Таким образом, все члены суммы делятся на

Для наглядности поместим все данные в таблицу

Сложив все члены таблицы в столбцах, получим сумму

Нам не потребуются значения коэффициентов

. Единственное, что следует здесь отметить, что все они положительные и все симметрично расположенные коэффициенты равны между собой.
Число членов в (3) всегда нечетно и равно

. И только два члена не кратны
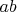
.
Если в (3) отбросить, например,

и разделить остаток на

, то получим

Отбросив в (3)

и разделив остаток на

, получим

Теперь, используя значения

и

, можем записать

Или

Поскольку

--- это четное число, то

при любом простом нечетном

(при


), следовательно,

Найдем теперь значение

.

Поскольку при любом нечетном

значения всех показателей степени в скобках -- это нечетные числа, то все скобки кратны

, следовательно

Сравнения (4) и (5) верны при любых

и

и при любых нечетных простых

. И это возможно только, если

и

.
Итак, окончательно получаем
![$$\begin{array}{lcl}
\sum_{i=1}^{p-1}\,\binom{p}{i}\,a^{p-i}\,b^i &=& pab(a+b)\left[b(a+b)M+a^{p-3}\right]\\
& = & pab(a+b)\left[a(a+b)N+b^{p-3}\right]\end{array}$$ $$\begin{array}{lcl}
\sum_{i=1}^{p-1}\,\binom{p}{i}\,a^{p-i}\,b^i &=& pab(a+b)\left[b(a+b)M+a^{p-3}\right]\\
& = & pab(a+b)\left[a(a+b)N+b^{p-3}\right]\end{array}$$](https://dxdy-01.korotkov.co.uk/f/0/9/8/098f999230d1f1ad6efd4f99d4a817eb82.png)
где
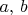
--- любые натуральные числа,

-- любое простое нечетное число, а

и

--- полиномы, значения которых зависят от
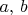
и

.
Таким образом, сумма

при любом нечетном простом

представляется в виде
![$$\begin{array}{lcl} a^p+b^p &=& (a+b)^p-p\,a\,b\,(a+b)\,\left[b\,(a+b)\,M+a^{p-3}\right]\qquad (6)\\
&=& (a+b)^p-p\,a\,b\,(a+b)\,\left[a\,(a+b)\,N+b^{p-3}\right]\end{array}$$ $$\begin{array}{lcl} a^p+b^p &=& (a+b)^p-p\,a\,b\,(a+b)\,\left[b\,(a+b)\,M+a^{p-3}\right]\qquad (6)\\
&=& (a+b)^p-p\,a\,b\,(a+b)\,\left[a\,(a+b)\,N+b^{p-3}\right]\end{array}$$](https://dxdy-01.korotkov.co.uk/f/c/a/7/ca720303e856c597e700789173db7b2982.png)
Вернемся к равенству (2). Далее нам потребуется выражение суммы справа. Оно легко получается из (6)
![$$\begin{array}{lcl} \sum_{i=0}^{p-1}(-1)^i\;a^{p-i-1}b^{i} &=& (a+b)^{p-1}-p\,a\,b\,\left[b\,(a+b)\,M+a^{p-3}\right]\qquad (7) \\
&=& (a+b)^{p-1}-p\,a\,b\,\left[a\,(a+b)\,N+b^{p-3}\right]\end{array}$$ $$\begin{array}{lcl} \sum_{i=0}^{p-1}(-1)^i\;a^{p-i-1}b^{i} &=& (a+b)^{p-1}-p\,a\,b\,\left[b\,(a+b)\,M+a^{p-3}\right]\qquad (7) \\
&=& (a+b)^{p-1}-p\,a\,b\,\left[a\,(a+b)\,N+b^{p-3}\right]\end{array}$$](https://dxdy-03.korotkov.co.uk/f/a/e/e/aee37e16869b43ab1a06be031543780982.png)
Наиболее простые частные решения получаются при

. При




При


.
![$$a^5+b^5=(a+b)^5-5ab(a+b)\left[b(a+b)+a^2\right]$$ $$a^5+b^5=(a+b)^5-5ab(a+b)\left[b(a+b)+a^2\right]$$](https://dxdy-02.korotkov.co.uk/f/1/1/b/11b3b913481a1c3db44e46e5072d673a82.png)
![$$ \sum_{i=0}^{4}(-1)^i\;a^{p-i-1}b^{i} = (a+b)^4-5ab\left[b(a+b)+a^2\right]$$ $$ \sum_{i=0}^{4}(-1)^i\;a^{p-i-1}b^{i} = (a+b)^4-5ab\left[b(a+b)+a^2\right]$$](https://dxdy-03.korotkov.co.uk/f/2/1/9/219c7542503a0a8b9c78e5e92850840182.png) 2. Доказательство великой теоремы Ферма.
2. Доказательство великой теоремы Ферма. Великая теорема Ферма (ВТФ) утверждает, что
Уравнение

не имеет решений в натуральных числах для любого натурального

.
При решении уравнения (8) можно ограничиться случаем, когда

и

являются взаимно простыми числами. Очевидно, если есть решение для взаимно простых

, то тройка

также будет решением при любом натуральном

. И, наоборот, если уравнение (8) не имеет решений, в которых значение переменных взаимно просты, то оно вообще не имеет натуральных решений.
Нет необходимости доказывать ВТФ для всех показателей степени
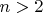
. Достаточно доказать, что уравнение (8) не имеет натуральных решений для

и

, где

--- любое нечетное простое число.
Если ВТФ верна для

, то она верна и для любого показателя степени, кратного 4-м.
А все остальные показатели степени
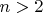
и не кратные

--м, --- это все нечетные числа и все четные числа типа

, где

--- любое нечетное натуральное число.
Все эти числа имеют общее свойство. Их каноническая форма обязательно содержит хотя бы одно нечетное простое число. Следовательно, если ВТФ верна для любого простого нечетного показателя степени

, то она верна и для любого не кратного 4-м показателя степени.
Для

ВТФ доказана самим Ферма. Для полноты картины приведем другое доказательство.
Вместо доказательства теоремы для уравнения

докажем более сильное утверждение: уравнение

не имеет натуральных решений. Действительно, если тройка натуральных чисел

является решением уравнения (9), то тройка

будет решением уравнения (10). И, наоборот, если уравнение (10) не имеет натуральных решений, то и уравнение (9) не имеет решений.
Сумма 4-х степеней двух нечетных чисел не может быть квадратом натурального числа, поскольку это число типа

, где

--- нечетное число. Поэтому в любом натуральном решении уравнения (10) значения

и

должны быть разной четности. Не теряя общности, будем считать значение

четным. Противоположенное допущение ничего не изменило бы: в этом случае достаточно было бы переименовать

в

и

в

.
Допустим тройка чисел

является решением уравнения (10).
Поскольку мы ищем решения, в которых

, можно записать уравнение (10) в виде

Отношение числителей и знаменателей в (11) равны

Два рациональных числа равны, если

. Т.е., должны выполняться два равенства

Подставив значение

из второго равенства в первое, получим

Поскольку

и
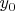
в решении являются взаимно простыми числами различной четности, то числитель и знаменатель дроби справа должны быть квадратами нечетных взаимно простых натуральных чисел. Только в этом случае значение

будет рациональным числом

Разность этих равенств приводит к уравнению

Это уравнение типа

Известно, что такие уравнения при четном натуральном

имеют бесчисленное множество натуральных решений со взаимно простыми значениями


где

--- любое натуральное число.
Нам не важны значения

и

в (12). Важен факт, что в любом решении значения

и

являются последовательными нечетными числами. Таким образом,

Подставив эти значения в (11)

мы приходим к противоречию: произведение двух последовательных нечетных чисел не может быть квадратом натурального числа.

Полученное противоречие доказывает, что отношение числителей и знаменателей в
(11) не равны (

). Равенство (11) неверно при любых натуральных
взаимно простых

. Наше предположение о наличии решения уравнения (10) было ошибочным. Уравнения (10) и (9) не имеют натуральных решений.
ВТФ верна для показателя степени

, и, следовательно, верна для любого показателя степени

, где

--- любое натуральное число.
Перейдем к доказательству ВТФ для всех простых показателей степени

.
По правилам форума сначала приведем доказательство для

.
Допустим, что тройка чисел

является решение уравнения (8)
при

. Тогда для этой тройки чисел должно выполняться равенство

Найдем отношения числителей и знаменателей в (13)

Два рациональных числа равны, если отношение их числителей и знаменателей равны (

). Т.е., должны выполняться два равенства

Возведя первое равенство в квадрат и подставив значение

из второго равенства, получим
![$$ k^3=\left[1-\frac{3\,x_0\,y_0}{(x_0+y_0)^2}\right]^2$$ $$ k^3=\left[1-\frac{3\,x_0\,y_0}{(x_0+y_0)^2}\right]^2$$](https://dxdy-01.korotkov.co.uk/f/4/d/e/4deda1d022ab920152359c1fb8efd33082.png)
Полученное равенство разрешимо относительно

в рациональных числах только в том случае, если выражение в квадратных скобках справа равно

и

.
Определим значение

, подставив эти значения в первое равенство в (14)
![$$ t^2z_0=(x_0+y_0)^2-3\,x_0\,y_0=(x_0+y_0)^2\left[1-\frac{3\,x_0\,y_0}{(x_0+y_0)^2}\right]=t^3(x_0+y_0)^2$$ $$ t^2z_0=(x_0+y_0)^2-3\,x_0\,y_0=(x_0+y_0)^2\left[1-\frac{3\,x_0\,y_0}{(x_0+y_0)^2}\right]=t^3(x_0+y_0)^2$$](https://dxdy-02.korotkov.co.uk/f/9/8/a/98a56cced6564bb73521e0c33c4465c982.png)

Подставив полученное значение

во второе равенство в (14)

мы получаем невозможное равенство

Полученное противоречие доказывает: отношение числителей и знаменателей в
(13) не равны, равенство (13) не выполняется при любых взаимно простых

, уравнение (8) при

не имеет натуральных решений. Сумма

при любых натуральных

не является кубом какого-либо натурального числа.
ВТФ верна для показателя степени

.
Доказательство для любого нечетного простого показателя степени

аналогично. Допустим, что тройка чисел

является решение уравнения (8) при

. Поскольку мы ищем решения, в которых

, можно записать уравнение (8) для этих значений в виде

Или с учетом (7)
![$$\frac{z_0}{x_0+y_0}=\frac{(x_0+y_0)^{p-1}-px_0y_0\,\left[y_0(x_0+y_0)M+x_0^{p-3}\right]}{z_0^{p-1}} \qquad (15)$$ $$\frac{z_0}{x_0+y_0}=\frac{(x_0+y_0)^{p-1}-px_0y_0\,\left[y_0(x_0+y_0)M+x_0^{p-3}\right]}{z_0^{p-1}} \qquad (15)$$](https://dxdy-04.korotkov.co.uk/f/f/2/9/f2923cb44e38852bd31b5cb12c02863582.png)
Отношение числителей и знаменателей в (15) равны
![$$k_1=\frac{(x_0+y_0)^{p-1}-px_0y_0\left[y_0(x_0+y_0)M+x_0^{p-3}\right]}{z_0};\;k_2=\frac{z_0^{p-1}}{x_0+y_0}$$ $$k_1=\frac{(x_0+y_0)^{p-1}-px_0y_0\left[y_0(x_0+y_0)M+x_0^{p-3}\right]}{z_0};\;k_2=\frac{z_0^{p-1}}{x_0+y_0}$$](https://dxdy-03.korotkov.co.uk/f/6/0/c/60c23723f1c897adec6a911c2859857482.png)
Два рациональных числа равны, если отношение их числителей и знаменателей равны (

). Т.е., должны выполняться два равенства
![$$kz_0=(x_0+y_0)^{p-1}-px_0y_0\left[y_0(x_0+y_0)M+x_0^{p-3}\right],\;k(x_0+y_0)=z_0^{p-1} \qquad (16)$$ $$kz_0=(x_0+y_0)^{p-1}-px_0y_0\left[y_0(x_0+y_0)M+x_0^{p-3}\right],\;k(x_0+y_0)=z_0^{p-1} \qquad (16)$$](https://dxdy-02.korotkov.co.uk/f/1/6/a/16a1f4e7733ca477db0ac06ddeb468b782.png)
Возведя первое равенство в степень

и подставив значение

из второго равенства, получим
![$$ k^p=\left\{1-\frac{px_0y_0}{(x_0+y_0)^{p-1}}\left[y_0(x_0+y_0)M+x_0^{p-3}\right]\right\}^{p-1}$$ $$ k^p=\left\{1-\frac{px_0y_0}{(x_0+y_0)^{p-1}}\left[y_0(x_0+y_0)M+x_0^{p-3}\right]\right\}^{p-1}$$](https://dxdy-03.korotkov.co.uk/f/6/2/4/62413424593f48d2e0d686cbc140a61082.png)
Полученное равенство разрешимо относительно

в рациональных числах только в том случае, если выражение в фигурных скобках справа равно

и

.
Определим значение

, подставив эти значения в первое равенство в (16)
![$$ t^{p-1}z_0=(x_0+y_0)^{p-1}-p\,x_0\,y_0\,\left[y_0\,(x_0+y_0)\,M+x_0^{p-3}\right]=t^p(x_0+y_0)^{p-1}$$ $$ t^{p-1}z_0=(x_0+y_0)^{p-1}-p\,x_0\,y_0\,\left[y_0\,(x_0+y_0)\,M+x_0^{p-3}\right]=t^p(x_0+y_0)^{p-1}$$](https://dxdy-04.korotkov.co.uk/f/7/b/5/7b580cf52682ce1ca963a4094ee29bca82.png)

Подставив полученное значение

во второе равенство в (16)

мы получаем невозможное равенство

Полученное противоречие доказывает: отношение числителей и знаменателей в
(15) не равны, равенство (15) не выполняется при любых взаимно простых

. Наше предположение о наличии решения уравнения (8) при любом нечетном простом показателе степени

было ошибочным. Сумма

при любых натуральных

и любом нечетном простом

не является

-й степенью какого-либо натурального числа.
ВТФ верна для уравнения (8), если показатель степени равен любому нечетному простому натуральному числу. Следовательно, она верна для любого показателя степени

, где

--- любое натуральное число.
ВТФ доказана.