Среднее расстояние между двумя случайными точками в квадрате

[melnikoff]

Чему равно среднее расстояние между двумя случайными точками в квадрате со стороной 1?

Попытка:
Нужно найти среднее значение величины $$D = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}, где $x_1, x_2, y_1, y_2$ – независимые и равномерно распределенные случайные величины на интервале $(0; 1)$.
Построим функцию распределения от $d = | x_1 - x_2|$:


$F(d) = 2d-d^2, \;\; 0 \leqslant d \leqslant 1$.
$F(d^2) = 2\sqrt{d^2}-d^2, \;\; 0 \leqslant d^2 \leqslant 1$.
Найдем также плотность вероятностей:
$p(d^2) = \frac{dF(d^2)}{dd^2}= \frac{1}{a\sqrt{d^2}}-\frac{1}{a^2}$.
И тут я затормозил.
Во-первых, меня очень смущает плотность вероятностей, так как она $ \rightarrow +\infty$ при $d^2 \rightarrow +0$.
А во-вторых, не могу понять как получить плотность вероятностей суммы двух одинаково распределенных случайных величин.
Прошу подсказки.

[ShMaxG]

Вы верно нашли функцию распределения расстояния между двумя точками на единичном отрезке, $F(d)$. Функцию распределения и плотность квадрата $d$ находить не нужно. По сути Вам нужно найти среднее $\sqrt{d_1^2+d_2^2}$ для независимых $d_1$ и $d_2$ с распределением, которое Вы нашли. Ну и вычисляйте в лоб это среднее, там будет двукратный интеграл, который вполне себе считается, хоть и после некоторой технической возни.

[GAA]

Обозначим $d = (x_2-x_1)^2$. Плотность этой случайной величины отлична от нуля при $0<x<1$: $f(x) = 1/\sqrt x -1$.
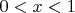
Плотность суммы можно вычислить продифференцировав функцию распределения
$F_{d_1+d_2} (t)= \iint_{x+y<t} (1/\sqrt x -1) (1/\sqrt y -1) dxdy.$
Сведём двойной интеграл к повторному. При расстановке пределов удобно рассмотреть два случая $0<t<1$ и $1<t<2$.
В первом случае область интегрирования можно записать в виде $0<x<t$, $0<y<t-x$.
$F_l(t) = \int_0^t (1/\sqrt x -1) dx \int_0^{t-x} (1/\sqrt y -1) dy = \pi t +\frac{t^2} 2 - \frac 8 3 t^{3/2}$.
$f_l(t) = \pi + t -4\sqrt t$.
В втором случае область интегрирования можно разбить на две части. Первая часть
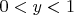
$0<x< t-1$, $0<y<1$ и вторая часть $t-1<x<1$, $0<y<t-x$.
Аналогично вычисляя функцию распределения и дифференцируя по $t$, получим плотность $f_h(t)$ для $1<t< 2$.
Зная плотности для всех значений аргумента, можно вычислить ожидание расстояния между двумя точками
$\int_0^1 \sqrt t f_l(t) dt + \int_1^2 \sqrt t f_h(t) dt.$
На этом пути на каждом шаге стандартные интегралы, но вычисления очень громоздкие.

[melnikoff]

ShMaxG, GAA разобрался. Спасибо!