Число 
довольно часто приводится в качестве примера очень большого числа, равного максимально возможной длине последовательности деревьев из вершин с возможными 3 цветами вершин, где

-ое дерево не имеет в качестве inf-вложения никакие из предыдущих

деревьев последовательности
В качестве примера везде приводится похожая картинка, подобная следующей, однако нигде не удалось найти описание, каким способом были получены эти самые деревья, составляющие начало вышеобозначенной последовательности

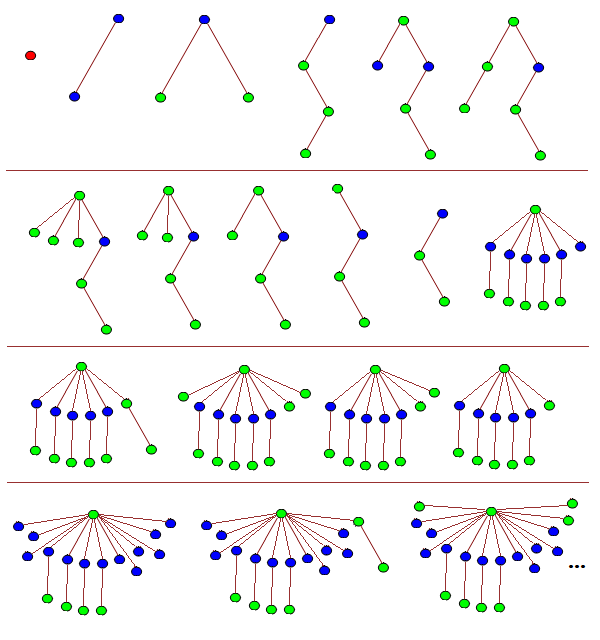 Вопрос
Вопрос - как получены эти начальные деревья последовательности и как генерировать следующие деревья? Кроме того, как определить, что эта последовательность деревьев образует начало
той самой последовательности длины

?
Понятное дело, что на приведенной картинке соблюдены требования - не более 3 цветов, не более

вершин в

-ом элементе последовательности и отсутствие inf-вложения слева направо - но ведь это не единственно возможный вариант начала последовательности, в том смысле, что она не продлится длиной

элементов, но вполне себе может продлиться

элементов, и только на

-ом дереве узнается, что она была неправильной, и чтобы достичь длины

, надо вернуться к началу и переделать ее элементы
Если на картинке все-таки правильные начальные элементы
той самой последовательности длины

, то как их получили и проверили на правильность?
Попытки подступиться к решению вопроса посредством гугления не увенчались успехом - попадаются только научно-популярные статьи с рассказами о невероятной величине числа

и одна и та же вышеприведенная картинка в различных дизайнерских вариациях
Если о настоящих статьях,
более-менее интересная нашлась эта (и посмотрена через scihub), но несмотря на сертифицированное программное доказательство, никаких формул конструктивного построения

-ых деревьев там не обнаружилось
Кстати еще вопрос вдогонку - существует ли доказательство конечности любого

без заигрываний с бесконечными ординалами? Если мне правильно удалось понять, то здесь, как и в случае с Гудстейном, доказательство через трансфинитные штуки