Запишем двоичное разложение

, обозначая нули кружочком

, а единицы вопросительным знаком

(считаем, что эти символы — альтернативные обозначения для нуля и единицы).
Тогда двоичное разложение любого

получится заменой каждого вопросительного знака либо на

, либо на

. А если из этого разложения убрать все кружочки

, получится разложение

. Поэтому в разложениях

и

одно и то же число единиц.
Например,

запишем как
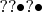
и перечислим все

и соответствующие

:
