Доброго времени суток!
Интересуюсь следующей проблемой, которую, формально, можно поместить и в раздел Computer Science (на усмотрение модераторов).
Даны две вещественные квадратные матрицы
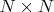
:

и

. К слову, эти матрицы суть

-овая и

-овая компоненты некоторого двухмерного векторного поля (на физическом языке это звучит как усредненное поперечное поле Пойнтинга), вычисленного в фиксированных узлах квадратной сетки соответствующей размерности.
Собственно, задача состоит в том, чтобы, имея лишь матрицы

и

восстановить структуру (фазовый портрет) следующей двумерной динамической системы:
![\[
\dfrac{\mathrm{d}}{\mathrm{d}\,\tau}\,\boldsymbol{r}=\boldsymbol{S}(\boldsymbol{r}),
\] \[
\dfrac{\mathrm{d}}{\mathrm{d}\,\tau}\,\boldsymbol{r}=\boldsymbol{S}(\boldsymbol{r}),
\]](https://dxdy-03.korotkov.co.uk/f/e/8/8/e8874e1f2bcb9d501556f1f73c44477682.png)
где

и

. Необходимо также уметь выделять особые траектории и точки ДС такие, как сепаратрисы, предельные циклы, фокусы и седла.
Может быть кто-нибудь подскажет, есть ли какие-либо библиотеки (лучше на Фортране), где можно отыскать процедуры для подобного анализа «дискретных» динамических систем. Если ничего похожего нет, посоветуйте с чего начинать.
Заранее благодарен