сжимаемые пространства

[redhat]

Опр. Метричесоке пространство $(M,\rho)$ называетс сжимаемым, если существует непрерывное отображение
$F:[0,1]\times M\to M$ такое, что
1) $F(t,\cdot):M\to M $ -- сжатие при всех $t<1$
2) $F(1,\cdot)=\mathrm{id}_M(\cdot)$

Задача. Доказать, что цилиндр $\{x^2+y^2=1,\quad |z|\le 1\}$ со стандартной метрикой из $\mathbb{R}^3$ несжимаем.

[nckg]

По идее это можно доказать от противного, используя один просто простой забавный факт. Нужно расмотреть нерастягивающее отображение $f(x,y,z)\colon M\to M$, у которого заведомо нет неподвижных точек на $M$ (например, поворот на угол $\varphi<2\pi$ вокруг оси $z$).

Однако мне этот способ не очень нравится, хотелось бы проверить само определение...

[nckg]

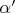
а) Покажем, что не существует сжимающего отображения $F$ окружности (с метрикой из $\mathbb R^2$) в себя. Пусть $R$ --- радиус окружности, $A$, $B$ и $C$ - вершины остроугольного треугольника, лежащие на ней, а $A'=F(A)$, $B'=F(B)$, $C'=F(C)$ --- их образы. Углы при этих вершинах обозначим соответственно $\alpha$, $\beta$, $\gamma$, $\alpha'$, $\beta'$ и $\gamma'$.
Т.к. $F$ --- сжимающее, то $A'B'<AB$ (аналогично для других сторон). Но по теореме синусов

$$\frac{AB}{\sin\alpha}=2R=\frac{A'B'}{\sin\alpha'},$$

след-но $\alpha'<\alpha$, аналогично $\beta'<\beta$, $\gamma'<\gamma$, так что сумма углов $\Delta A'B'C'$ меньше $\pi$. Противоречие.

б) Случай цилиндра можно свести к окружности. Пусть $P\colon \mathbb R^3\to \mathbb R^2$ --- проекция точек пространства на плоскость $z=0$. Пусть $F$ --- сжимающее отображение $M$ в себя. Тогда $\widetilde F = P \circ F$ --- сжимающее отображение окружности $M \cap \{z=0\}$ в себя.

Таким образом, нелья выполнить пункт (1) Вашего определения.