Сомик писал(а):
Имеется следующая задача

при

Где бы можно было посмотреть алгоритмы ее решения?
Ясно, что можно раскрыть все модули, и тогда каждый раз будем получать задачу линейного программирования, но это дает экспоненциальный по

перебор.
Можно делать тоже, что и в симплекс-методе: искать решения, с все более возрастающим значением целевой функции. Но даже в задачах ЛП максимальное число итераций оценивается сверху как

- что растет экспоненциально от числа равенств

. Есть правда полиномиальные алгоритмы решения ЗЛП, но они сложны.
При фиксированном значении всех переменных, кроме одной

, целевая функция принимает вид

, где

Значит, график целевой функции от одной из переменных

представляет собой ломаную линию и достигает максимума, либо в крайней точке

, либо в одной из точек точке излома

(

), то есть в некой точке

. Сменяем значение (на

) той переменной

, которая дает наибольшее увеличение целевой функции

, при условии, что оно больше нуля. И так повторяем итерации, пока это наибольшее увеличение целевой функции не станет равным нулю

. Значит, мы достигли локального максимума. Если между любыми двумя допустимыми точками

и

существует ограниченный условиями

ломаный путь с отрезками параллельными осям

и монотонный по значениям целевой функции (это некий аналог условия выпуклости задачи), то локальный максимум является и глобальным.
Увы, не могу сформулировать для этой задачи понятие крайней точки по аналогии с ЗЛП, тогда можно было бы сформулировать условие выпуклости с произвольно направленными отрезками, и, вероятно, доказать выпуклость задачи для общего случая.
Вот процедура, написанная в
Мапле 8, от аргументов:
число переменных

, число модулей в целевой функции

, матрица коэффициентов A=[seq([seq(A[j,i],i=1..n)],j=1..k)];
и дающая: число итераций

от начальных значений переменных
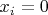
до локально-максимального решения, решение

, значение максимума целевой функции

:
> zklp:=proc(n,k,A)
> local a,b,c,i,j,l,m,r,u,v,x,y,z;
> a:=[seq([seq(convert(A[j,i],rational,exact),i=1..n)],j=1..k),seq([seq(1,i=1..n)],j=1..2)]; c:=[seq(0,i=1..k+2)]; x:=[seq(0,i=1..n)]; y:=[seq(0,i=1..n)]; z:=[seq(0,i=1..n)]; m:=0; r:=0;
> b:=false; for i to n do for j to k do if a[j,i]<>0 then b:=true; j:=k; i:=n fi od od;
> while b do for i to n do c[k+1]:=x[i]; c[k+2]:=x[i]-1; y[i]:=0; z[i]:=0; for j to k+2 do if a[j,i]<>0 then u:=-c[j]/a[j,i]; if 0<=u and u<=1 then v:=add(abs(c[l]+a[l,i]*u),l=1..k); if v>z[i] then y[i]:=u+x[i]; z[i]:=v fi fi fi od od; l:=0; v:=0; for i to n do if z[i]>v then l:=i; v:=z[i] fi od; if z[l]>m then for j to k do c[j]:=c[j]+a[j,l]*(y[l]-x[l]) od; x[l]:=y[l]; m:=z[l]; r:=r+1 else b:=false fi od;
> RETURN(r,x,m)
> end:
прим: функция

преобразует числа

вещественного типа в рациональную десятичную дробь, а рационального и целого типа не изменяет; использована, чтобы пресечь округления.