Матричные операции для вычисления радикала

[dmd]

Вот здесь показывается пример вычисления $5^{1/5}$.

Помогите это расшифровать и повторить в W.Mathematica или в pari/gp.

[Xaositect]

Рассмотрим матрицу $M = \begin{bmatrix} 0 & 1 & 0 & 0 & \dots & 0 \\ 0 & 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 0 & 1 & \dots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \dots & 1 \\ x & 0 & 0 & 0 & \dots & 0 \end{bmatrix}$.
Видно, что характеристический многочлен этой матрицы будет $\pm(\lambda^n - x)$, собственные значения - это все комплексные значения корня $\sqrt[n]{x}$, которые мы обозначим $\alpha_k = \sqrt[n]{x} e^{\frac{2\pi k i}{n}}$, $k = 0, 1, \dots, n - 1$.

Отсюда идея - можно искать значение $\sqrt[n]{x}$ с помощью алгоритмов поиска собственных значений или векторов. Однако наша матрица для этих алгоритмов плоха - у нее все собственные значения одинаковы по абсолютной величине. Чтобы избавиться от этой проблемы, мы можем "выпятить" интересующее нас собственное значение $\sqrt[n]{x}$, прибавив к матрице единичную. Максимальное по модулю собственное значение матрицы $I + M$ будет $1 + \sqrt[n]{x}$, и по теореме Фробениуса-Перрона матричная последовательность $(I + M)^k$ будет асимптотически приближаться к $C (1 + \sqrt[n]{x})^k u v^T$, где $u$ - собственный вектор, соответствующий $1 + \sqrt[n]{x}$, а $v$ - аналогичный собственный вектор матрицы $(I + M)^{T}$.

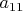
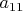
Cобственные векторы будут иметь вид $u = (1, \sqrt[n]{x}, \sqrt[x]{x^2}, \dots, \sqrt[n]{x^{n-1}})^T$ и $v = (1, \sqrt[n]{x^{-1}}, \sqrt[x]{x^{-2}}, \dots, \sqrt[n]{x^{-(n-1)}})^T$, так что можно найти приближенное значение $\sqrt[n]{x}$, вычислив $A = (I + M)^N$ и поделив $a_{11}$ на $a_{12}$ или $a_{21}$ на $a_{11}$. Или можно найти приближенное значение $1 + \sqrt[n]{x}$, поделив соответствующие элементы $(I + M)^{N + 1}$ и $(I + M)^N$

Если вычислять степени матриц двоичным алгоритмом, то сходимость будет квадратичная. Но метод Ньютона, мне кажется, будет лучше.