Перестановка, максимизирующая сумму произведений

[z_en_t]

Помогите, пожалуйста, с такой задачей. Ее нужно решить программным путем за приемлемое время.

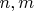
Пусть $n, m$ - натуральные числа (число $n$ обычно порядка нескольких сотен или даже тысяч);

$x, y$ - известные (заданные) двумерные массивы (т.е. матрицы) размера $n \times m$, элементы которых - нули или единицы (то есть двоичные массивы);

$\sigma$ - перестановка множества $\{1,2, \ldots, n\}$.

Требуется найти все перестановки $\sigma^\ast$, максимизирующие следующую сумму:

$$ \sum_{i=1}^n \sum_{j=1}^m x_{\sigma(i),j}y_{i,j} \rightarrow \max_{\sigma}. \eqno{(1)} $$

Можно сначала для простоты найти хотя бы одну такую перестановку, а затем пытаться найти уже все такие перестановки.

Проблема в том, что перебрать тупым полным перебором все $n!$ перестановок невозможно. Нужно придумать алгоритм, который позволит решить эту задачу за приемлемое время.

Упрощенная задача для случая одномерных двоичных массивов $x$ и $y$, состоящих из $n$ элементов

$$ \sum_{i=1}^n x_{\sigma(i)}y_{i} \rightarrow \max_{\sigma} \eqno{(2)} $$

легко решается с помощью перестановочного неравенства (транснеравенства).

Но что делать с задачей (1)? Там ведь одно $\sigma(i)$ присутствует сразу в $m$ слагаемых. И задача вроде как не расщепляется, не сводится к задачам типа (2).

[worm2]

1) Тут нужно сделать формальное замечание, что может случиться так (например, если все числа равны 0), что любая перестановка доставляет максимум, и простое их перечисление неизбежно приведёт к сложности $O(n!)$

2) Нахождение одного решения, похоже, сводится, к задаче о назначениях с квадратной матрицей $A_{pq}=-\sum\limits_{j=1}^m x_{pj} y_{qj}, \quad p, q = 1, \dots, n$ (минус, потому что в задаче о назначениях нужно минимизировать целевую функцию, а нам нужно максимизировать). По слухам, эта задача эффективно решается венгерским алгоритмом.