Всех приветствую. Хочу строго доказать, что сумма, вычитание, произведение и частное случайных величин есть случайная величина.
Посмотрел доказательство в 1-м томе Ширяева(гл.2, пар.4), честно, не понравился подход. Хотелось бы отталкиваться от базовых определений.
Мои рассуждения таковы. Приведу пример для суммы.
Рассмотрим случайные величины

,

, заданные на



- случайная величина, если прообраз любого борелевского множества принадлежит сигма-алгебре.
Берем любое

.

Возьмем

,
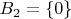
. Оба этих множества борелевских. Получаем:


,

- случайный величины, поэтому

,

. А значит и пересечение принадлежит сигма-алгебре

. Таким образом

- случайная величина.
Для вычитания аналогично. Для произведения и частного можно взять

.
Есть ли проблема в этих рассуждениях? Заранее спасибо.