(Предупреждение: далее, вроде бы, одно и то же написано 2 раза, потом я это перечитаю и исправлю, а пока не относитесь с доверием, если читаете; и извините.)
А мне, пожалуй, больше нравится сначала доказывать "геометрический" вариант теоремы об интегрируемости, а потом выводить из него единственность. Делать оценки при этом необязательно, всё уже сделано
до нас при доказательстве теоремы о локальном решении задачи Коши и теоремы об обратной функции.
Зафиксируем порядок гладкости

или

.
1. Предварительные сведения1.1. Теорема о постоянном ранге. Пусть

,

— открытые подмножества

и
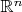
соответственно (или

-гладкие многообразия размерности

и

соответственно),

—

-гладкое отображение, дифференциал которого имеет постоянный ранг

. Тогда для любой

можно выбрать

-гладкие координаты около

и около

так, что в этих координатах

будет иметь вид

.
Точнее говоря, найдутся открытые окрестности

точки

и

точки

с

, а также

-диффеоморфизмы

,

и

,

, где

и

— открытые окрестности нуля в

и
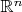
соответственно, такие что

совпадает с ограничением на

вышеописанного стандартного отображения

ранга

.
(В частном случае

это теорема об обратной функции.)
1.2. Теорема о выпрямлении векторного поля. Пусть

— открытое подмножество

(или

-мерное

-гладкое многообразие),

—

-гладкое векторное поле на

. Пусть

,

. Тогда около

можно выбрать

-координаты

так, что в этих координатах

будет равно

.
Литература: Арнольд, Обыкновенные дифференциальные уравнения.
Teschl, Ordinary differential equations and dynamical systems.
2. Выпрямление распределений2.1. Лемма. Пусть

—

-гладкое векторное подрасслоение ранга

в тривиальном расслоении ранга

над интервалом

. Предположим, что у любого

-сечения

,

производная

при всех

. Тогда

постоянно (совпадает с

для какого-то

-мерного векторного подпространства

).
Доказательство: Выбором тривиализации

задача сводится к следующей. Задано линейное вложение

,

-гладко зависящее от

, причём известно, что для любого гладкого отображения

выполняется

для всех

; по правилу дифференцирования композиции, это условие эквивалентно включению

для всех

. Надо доказать, что образ

не зависит от

.
Рассмотрим отображение

,

. Его матрица Якоби в точке

равна

, поэтому имеет постоянный ранг

.
По теореме о постоянном ранге, образ

есть

-мерное подмногообразие в

; с другой стороны, он равен

. Значит, все

одинаковые.
 2.2. Теорема Фробениуса.
2.2. Теорема Фробениуса. Пусть

— открытое подмножество

(или

-мерное

-гладкое многообразие),

—

-гладкое распределение на

ранга

. Предположим, что
 инволютивно,
инволютивно, то есть для любых двух

-гладких векторных полей

и

на

со значениями в

их коммутатор
![$[u,v]$ $[u,v]$](https://dxdy-02.korotkov.co.uk/f/5/5/f/55fd72205ba09006c8b4d568ad5b5a3c82.png)
тоже принимает значения в

. Тогда

локально является касательным распределением к слоям некоторой

-субмерсии (то есть
вполне интегрируемо).
Точнее говоря, у любой

найдётся открытая окрестность

и

-субмерсия

, такая что

. (По теореме о постоянном ранге отсюда сразу следует, что

локально

-изоморфно

, где

стандартно вложено в

:

.)
Доказательство:- Зафиксируем
 . Выберем незануляющееся сечение
. Выберем незануляющееся сечение  около
около  . По теореме о выпрямлении векторного поля мы можем считать (уменьшив
. По теореме о выпрямлении векторного поля мы можем считать (уменьшив  , если это нужно), что
, если это нужно), что  и выбранное сечение есть
и выбранное сечение есть  , где
, где  — интервал,
— интервал,  — координата на
— координата на  .
.
- Рассмотрим подрасслоение
 расслоения
расслоения  , состоящее из векторов, касательных к слоям проекции
, состоящее из векторов, касательных к слоям проекции  ; то есть
; то есть 

 и
и  .
.
Для любого  выполнено
выполнено ![$[\partial_t,v]t=\partial_t(vt)-v1=0$ $[\partial_t,v]t=\partial_t(vt)-v1=0$](https://dxdy-01.korotkov.co.uk/f/0/7/3/0739392435fde11047f7ca34b225cf7c82.png) , поэтому
, поэтому ![$\mathrm{Lie}_{\partial_t}v=[\partial_t,v]\in\Gamma(\widetilde E)$ $\mathrm{Lie}_{\partial_t}v=[\partial_t,v]\in\Gamma(\widetilde E)$](https://dxdy-02.korotkov.co.uk/f/d/5/9/d590a1668cb6a47346b750735cbc496282.png) . По лемме,
. По лемме,  постоянно на каждом слое проекции
постоянно на каждом слое проекции  .
.
То есть  , где
, где  — какое-то распределение на
— какое-то распределение на  , и любое вложение
, и любое вложение  устанавливает биекцию между сечениями
устанавливает биекцию между сечениями  и постоянными по
и постоянными по  сечениями
сечениями  .
.
- Для любых
 выполнено
выполнено ![$[u,v]t=u(vt)-v(ut)=0$ $[u,v]t=u(vt)-v(ut)=0$](https://dxdy-04.korotkov.co.uk/f/f/3/6/f36e04a9ce071e3e0e6605a8f59519aa82.png) . Поэтому
. Поэтому  инволютивно.
инволютивно.
- Теперь мы докажем теорему индукцией по рангу
 . Для
. Для  она сразу получается из теоремы о выпрямлении векторного поля: выберем незануляющееся локальное сечение, в выпрямляющих координатах натянутое на него распределение касательно к слоям субмерсии
она сразу получается из теоремы о выпрямлении векторного поля: выберем незануляющееся локальное сечение, в выпрямляющих координатах натянутое на него распределение касательно к слоям субмерсии  .
.
Пусть теорема доказана для  . Тогда есть субмерсия
. Тогда есть субмерсия  , касательное распределение к слоям которой есть
, касательное распределение к слоям которой есть  (возможно, придётся предварительно уменьшить
(возможно, придётся предварительно уменьшить  ). Тогда
). Тогда  — субмерсия, касательное распределение к слоям которой есть
— субмерсия, касательное распределение к слоям которой есть  .
. 
3. Потоки векторных полей(Оффтоп)
Пусть

— открытое подмножество

,

— векторное поле на

.
3.1. Понятие потока. Пусть

,

. Предположим, что существует интервал

, содержащий

и

, и функция

, удовлетворяющая дифференциальному уравнению

(

) и отображающая

в

.
Тогда её значение в точке

называется потоком

из

за время

и обозначается

.
3.2. Локальное существование и единственность. Теорема о локальном решении обыкновенного дифференциального уравнения говорит, что если

локально липшицево (например,

-гладко), то для любой

найдётся окрестность

точки

, такая что

существует и однозначно определено при всех

, причём оно непрерывно на

и

-гладко, если


-гладко.
Для

-векторных полей это сразу получается из теоремы о выпрямлении: для незануляющихся — непосредственно, а общий случай легко сводится к этому, см. далее. То есть для

-гладких полей теорема о выпрямлении есть эквивалентная формулировка теоремы о локальном существовании и единственности решения задачи Коши для обыкновенного дифференциального уравнения и гладкой зависимости от начального условия.
Замечание: композиции потоков. Отсюда следует, что если

— открытое подмножество

,

,

— локально липшицевы векторные поля на

, то найдётся окрестность точки

, такая что для всех

из этой окрестности определено

. Действительно, каждое из отображений

непрерывно, определено в некоторой окрестности точки

и сохраняет эту точку, значит, то же верно и для композиции.
3.3. Глобальная единственность. Из этой локальной теоремы следует, что если

локально липшицево и

существует для каких-то

и

, то только одно.
Доказательство: Для

это верно по определению; можем считать, что

(в противном случае заменим

на

). Зафиксируем интервал

из определения и рассмотрим

— множество таких

, что

единственно для всех

.

открыто в

по локальной теореме, замкнуто в силу непрерывности решения и непусто, так как содержит

; поскольку

связно, то

с ним совпадает.

Поэтому если

локально липшицево, то существует единственное максимальное открытое подмножество

(включающее

), на котором определён поток

.
3.4. Расширение фазового пространства. Пусть

— открытое подмножество

(или

-гладкое

-мерное многообразие),

—

-гладкое векторное поле на

. Его можно продолжить до векторного поля

,

. Поток

(части равенства одновременно определены или не определены). Поэтому изучать

— это примерно то же самое, что изучать

. При этом

нигде не
обращается в 0, поэтому к нему, например, применима теорема о выпрямлении. Отсюда для любой точки

сразу видно локальное существование, единственность и

-гладкость потока

.
Аналогично, если изначально задано

векторных полей

, то можно изучать вместо них

,

(единица на

-м месте). Они в каждой точке ненулевые и линейно независимые. (Так же можно поля, зависящие от времени или от параметров, превратить в независящие.)
3.5. Потоки коммутирующих полей локально коммутируют. Пусть

— открытое подмножество

,

,

—

-гладкие векторные поля на

, все
![$[v_i,v_j]=0$ $[v_i,v_j]=0$](https://dxdy-01.korotkov.co.uk/f/4/0/e/40e7242cb41eed73479524494778d9ce82.png)
тождественно. Тогда существует

, такое что при всех

определено выражение

для любой перестановки
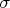
и все они имеют одинаковое значение.
Доказательство: Достаточно доказать при

, потому что любую перестановку строки можно сделать последовательными перестановками соседних элементов.
По наблюдению о расширении фазового пространства, достаточно это доказать в предположении, что

нигде не обращается в

. Поэтому по теореме о выпрямлении можно считать, что

, уменьшив при необходимости

. Мы знаем, что

определено при

для некоторого

. Зануление коммутатора в случае

означает, что

не зависит от

. Поэтому
поток 
(сдвиг по

)
сохраняет интегральные кривые  .
.  3.6. Глобальная коммутативность потоков.
3.6. Глобальная коммутативность потоков. Пусть

— открытое подмножество в

(или

-гладкое

-мерное многообразие),

,

—

-гладкие векторные поля на

, все
![$[v_i,v_j]=0$ $[v_i,v_j]=0$](https://dxdy-01.korotkov.co.uk/f/4/0/e/40e7242cb41eed73479524494778d9ce82.png)
тождественно,

— отрезки вида
![$[0,...]$ $[0,...]$](https://dxdy-01.korotkov.co.uk/f/4/7/6/47640a5a58936fb48dc60ad1dbd7161582.png)
. Предположим, что

определено для всех

. Тогда для любой перестановки
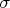

тоже определено для всех

и равно тому же самому.
Доказательство: Опять достаточно доказать для

. Обозначим

,

. Зафиксируем

. Рассмотрим для каждой точки

замкнутого прямоугольника

, ограниченного прямыми

,

,

, открытый квадрат с центром в

и со сторонами длины

, параллельными сторонам

, где

означает число

из предыдущей леммы для точки

вместо

. Эти квадраты образуют открытое покрытие

, и так как

компактен, то он покрывается конечным количеством этих квадратов. Выберем положительное число

, меньшее половины длины стороны самого маленького из них, и разобьём

вертикальными и горизонтальными прямыми на прямоугольники

со сторонами

, меньшими

. Теперь напишем

. Предыдущая лемма позволяет обменивать

на

(выражение, полученное такой заменой, будет определено и равно исходному). Делая такие
перестановки, мы получим

, а это равно

.
 Замечание.
Замечание. Отсюда сразу следует, что если поля

и

полны (например, это верно, если их носители компактны) и
![$[u,v]=0$ $[u,v]=0$](https://dxdy-01.korotkov.co.uk/f/0/f/3/0f38ef3ec32fb5c6486802514e88417982.png)
тождественно, то их потоки глобально коммутируют:

для всех

и

. Для неполных полей равенство может и не выполняться, даже если обе его части определены (пример: Lee, Introduction to smooth manifolds, 2nd edition, problem 9-19).
Замечание. Дифференциал отображения

из предыдущего предложения переводит

в

, потому что

.
Пусть

— открытое подмножество

(или

-мерное

-гладкое многообразие),

— попарно коммутирующие

-гладкие векторные поля, линейно независимые в каждой точке

. Тогда около каждой точки

есть

-координаты

, такие что в этих координатах

и

для всех

.
Доказательство: Зафиксируем

. По теореме Фробениуса можно считать, что

,

и все

линейно выражаются (с

-коэффициентами) через

. Отображение

определено около

(доказано выше),

-гладко (как композиция гладких отображений), переводит

при

в

(следует из коммутативности потоков, см. выше), сохраняет

(так как тождественно при

), значит, имеет невырожденный дифференциал в

, поэтому задаёт локальные координаты около

(по теореме об обратной функции).
 4.2. Cформулируем это в терминах дифференциальных уравнений.
4.2. Cформулируем это в терминах дифференциальных уравнений. Пусть

— область в

,

—

-гладкие функции, все коммутаторы
![$[v_i,v_j]=0$ $[v_i,v_j]=0$](https://dxdy-01.korotkov.co.uk/f/4/0/e/40e7242cb41eed73479524494778d9ce82.png)
тождественно.
- Фиксируем
 . Найдётся область
. Найдётся область  , содержащая
, содержащая  , и
, и  -функция
-функция  , такая что
, такая что  для всех
для всех 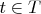 и
и  .
.
Любые 2 такие  и
и  (с областями опредления
(с областями опредления  и
и 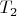 ) совпадают на
) совпадают на  .
.
В частности, среди всех таких  есть единственная функция
есть единственная функция  с максимальной областью определения
с максимальной областью определения  .
.
- Соберём все
 из п. 1 в функцию
из п. 1 в функцию  , определённую на подобласти
, определённую на подобласти  (
( 

 и
и  ). Эта
). Эта 
 -гладкая. Если все
-гладкая. Если все 
 -гладкие (
-гладкие ( или
или  ), то и
), то и  тоже.
тоже.
(Желающие могут добавить сюда зависимость от «начального времени» — т. е.

, — зависимость

от

и перестановочность производных по

с производными по

.)
Доказательство: По замечанию о расширении фазового пространства можно считать, что

в каждой точке линейно независимы (коммутативность не испортится). По предыдущей теореме можно считать, что

— окрестность

в

,

. Локальное существование:

. Локальная единственность: рассмотрим проекцию

,

. Посткомпозиция

с этой проекцией имеет нулевой дифференциал, следовательно, она отображает всё в точку по
теореме о ранге. Значит,

постоянны. Поэтому можно считать, что

. Если есть две такие

, то их разность имеет нулевой дифференциал, следовательно, постоянна на любой прямой через

, следовательно, постоянна и равна

около

.
