Если алгоритм кого-то заинтересует, то после окончания конкурса я его выложу.
Yes, I would be interested. I realized that my incremetal method is the same what dmd describes in his post. You can start with the solution with N=16 and 0 triangles. By adding point after point you get solutions for N=17, 18, 19, 20, 21, 22, 23, 24 with 5, 10, 15, 20, 25, 33, 41, 50 triangles. The solutions get worse than the default method for N>=22. It is interesting that all solutions in this series up to N=21 have only triangles of a single color, which is not the case for N>=22.
If you start with the default solution for some N, the incremental method obviously gives the default solution for N+1. And it seems, that that all known best solutions for all N >=22 are the default solutions. So basically, solutions with fewest (currently known) triangle numbers all can be generated with the incremental method from the two chains
N=16 (0 triangles)->17->18->19->20->21 and
N=22(default solution)->23->24->25-> ..... infinity
It also is interesting that though the N=19 solution obtained incrementally has 15 triangles of one color, there also exists a solution with 5 triangles of each color which I never happened to see with simulated annealing. Plotting only the triangles the solution looks like this:
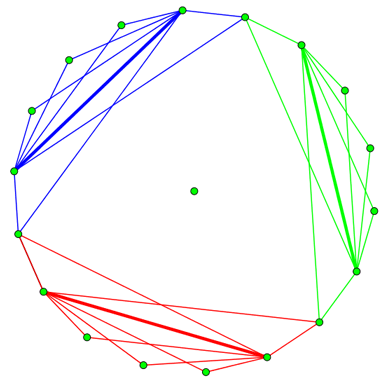
The thick lines are the base of all triangles of one color.
It is possible that this approach also will give the configuration with a minimum number of monochromatic triangles for all N greater some N0. But for lower N this does not work very well. With K=4 and N=48 we already would have 16 monochromatic triangles, but for K=4 even for N=50 there exists a coloring without any mono triangles.
I realized that this method is not as bad as I thought with K=4 colors. The number of triangles with m=Floor(N/16) and r = Mod(N,16) is
r*Binomial(m+1,3)+ (16-r)*Binomial(m,3)
and for N= 55, 56, 57 it gives 37, 40, 43 triangles. If you compare this with the data Martin Piotte gave in
AZsPCs@groups.io it seems that the default method with 4 colors gives good values for N>=56.
Код:
n | number of monochromatic triangles
------+----------------------------------
<= 50 | 0
51 | 1
52 | 4
53 | 10
54 | 21
55 | 32
56 | 40
57 | 43